هندسه دیفرانسیل در میپل (قسمت چهارم)
قسمت اول
- دوم
-
سوم
دستگاه مختصات قطبی
طول خم

انحنا

اسپیرال لگاریتمی

لمنیسکات

دلگون

مارپیچ ارشمیدس

هندسه دیفرانسیل منیفلدها و تانسورهای متریک:
خمینه
یا منیفلد
(انگلیسی: Manifold)؛ فضای توپولوژی است که در هر نقطه بهصورت موضعی
شبیه فضای اقلیدسی است. به طور دقیقتر، هر نقطه از فضای n-بعدی دارای
همسایگی هومئومورف با فضای اقلیدسی n بعدی است؛ بنابراین اگر بخواهیم
دقیقتر بگوییم یک منیفلد بر اساس توصیف فوق یک n-منیفلد است.

هومئومورفیسم
(به انگلیسی: Homeomorphism) (برای آن معادلهایی چون
همسانریختی
هم پیشنهاد شده)، در مکانشناسی، یکریختی (ایزومورفیسم) ویژهای میان
فضاهای مکان شناختی است که خواص مکان شناختی را حفظ میکند. دو فضا با
یک همسانریختی میان آنها، همسان ریخت نامیده و از دیدگاه توپولوژیکی،
یکسان در نظر گرفته میشوند. به سخن دیگر، یک فضای توپولوژیکی، یک شیء
هندسی است و همسانریختی نیز خمکردن و کشیدن پیوسته شیء و تبدیل آن به
یک شیء جدید است؛ بنابراین، یک مربع و یک دایره همسان ریخت هستند؛ اما
یک مربع و یک چنبره، با هم همسان ریخت نیستند. اغلب به شوخی گفته
میشود که توپولوژیستها نمیتوانند فنجان قهوه خود را از پیراشکی
تشخیص دهند؛ چرا که یک پیراشکی را میتوان بهگونهای پیوسته تغییر شکل
داد تا به شکل یک فنجان قهوه تبدیل شود. به طور شهودی، میتوان گفت که
یک همسانریختی، نقاط شیء نخست را که به یکدیگر نزدیک هستند، به نقاطی
از شیء دوم مینگارد که به یکدیگر نزدیک هستند، و نقاطی در شیء اول را
که به یکدیگر نزدیک نیستند، به نقاطی در شیء دوم مینگارد که به یکدیگر
نزدیک نیستند. توپولوژی مطالعه خواصی از اشیا است که با بهکاربردن
همسانریختیها، تغییر نمیکنند.

یک منیفلد یکبعدی شامل خطوط
و دوایر است، اما شکل عدد هشت انگلیسی منیفلد یکبعدی نیست (چرا که در
مرکز عدد هشت انگلیسی دو خم با هم برخورد کردهاند و هیچ همسایگی آن با
فضای اقلیدسی یکبعدی هومئومورف نیست). منیفلدهای دوبعدی را رویه (سطح)
مینامند. بهعنوان مثالی از منیفلدهای دوبعدی میتوان به صفحه، کره،
چنبره اشاره کرد که تمام آنها را میتوان در فضای سهبعدی نشاند (بدون
این که از خودشان عبور کنند) اما بطری کلاین و صفحهتصویری حقیقی هم
منیفلد دوبعدی هستند که نمیتوانند برعکس مثالهای قبلی در فضای
سهبعدی بنشینند (immersion) چون در این صورت الزاماً خودشان را قطع
خواهند کرد.

گرچه که یک منیفلد بهصورت
موضعی شباهت به فضای اقلیدسی دارد، یعنی هر نقطه از آن همسایگی ای دارد
که با یک زیرمجموعه باز از فضای اقلیدسی هومئومورف است، اما به طور
سراسری ممکن است با فضای اقلیدسی هومئومورف نباشد. بهعنوانمثال، رویه
کره با صفحه اقلیدسی هومئومورف نیست، چرا که (علاوه بر خواص دیگر)
خاصیت توپولوژیکی سراسری فشردگی را داشته درحالیکه فضای اقلیدسی
متناظر با آن فشرده نیست، اما در یک ناحیه از کره میتوان بهوسیلهٔ
نگاشتهای تصویری چارتهایی ساخت بین آن ناحیه از کره و صفحه دوبعدی
اقلیدسی. زمانی که یک ناحیه در دو چارت همسایه پدیدار گردند، آن دو
نمایش به طور دقیق با هم یکی نمیشوند و تبدیلی بینشان نیاز است که به
آن نگاشت انتقال میگویند.
مفهوم منیفلد در بسیاری از
بخشهای هندسه و ریاضی - فیزیک مدرن نقش محوری دارد، چرا که امکان
توصیف و فهم ساختارهای پیچیدهتر را بهوسیله خواص توپولوژیکی موضعی
سادهتر هندسهٔ اقلیدسی را میدهد. منیفلدها به طور طبیعی در حل مجموعه
دستگاههای معادلاتی و نمودار توابع ظاهر میشوند.
منیفلدها را میتوان با
ساختارهای اضافی مجهز کرد. یک دسته منیفلدهای مهم، منیفلدهای دیفرانسیل
پذیر هستند؛ این ساختار دیفرانسیل پذیر امکان انجام حساب دیفرانسیل و
انتگرال را بر روی منیفلدها میدهد. یک متر
ریمانی روی منیفلد امکان میدهد تا فواصل و زاویهها را اندازهگیری
کرد. منیفلدهای سیمپلکتیک بهعنوان فضای فازی در فرمالیسم
همیلتونی مکانیک کلاسیک عمل میکنند، درحالیکه منیفلدهای لورنتزی فضا
- زمان را در نسبیت عام مدل میکنند.
اگر خیلی ساده گفته باشیم تا اینجا موجودات هندسی ما داخل یک
دستگاه مختصات دکارتی با محورهای عمود بر یکدیگر بودند یا اینکه تصور
میشدند. یعنی سنجه و مقیاس یا متریک ما دستگاههای مختصات دکارتی،
کروی، قطبی یا استوانهای بودند و ما تغییرات داخلی شکل هندسی را نسبت
به آنها برسی میکردیم. اما در هندسه تانسوری یا ریمانی دستگاه مختصات
ما خودش خم یا انحنا برمیدارد و خمینهها یا منیفلدها نسبت به آن
متریک خمینه سنجیده میشوند. قبل از این ما فکر میکردیم که یک کره،
یکشکل سهبعدی است؛ ولی بعدازاین دوبعدی فرض میشوند. چرا؟
برای اینکه طرز فکر و اندیشهها متفاوت شده است. ریمان بر این باور بود
که ما از دوران کودکی روی سطح کره زمین زندگی کردیم و فکر و تصور کردیم
که این یک سطح صاف و دوبعدی است؛ ولی بعداً فهمیدیم که در دستگاه
مختصات دکارتی سهبعدی است. چون از خارج به آن نگاه کردیم. ولی او
باورداشت که بهتر است از همان طرز فکر قبلی استفاده کنیم و ما نباید
اشکال هندسی را از بیرون آن تحلیل کنیم؛ بلکه هم خودمان و هم دستگاه
مختصاتمان یعنی متریک، باید به خود خمینه مهاجرت کنیم و دنیایی جدید را
تجربه و در آنجا زندگی کنیم. یعنی بعدازاین باید روی خمینهها راه رفت،
زندگی کرد، خوابید و غذا خورد و... چون در حال و گذشته هم
اینچنین بودهایم و هستیم؛ یعنی ما روی یک خمینه متولد شده و روی یک
خمینه فوت میکنیم. تجربه خمینههای دیگر برای ما میتواند تنوعی شگرف
بوده باشد.
ولی برای ریمان و خیلیها سؤال این بود که ما از کجا بفهمیم که
روی یک خمینه هستیم بدون اینکه از بیرون به آن نگاه کنیم؟
پاسخ ساده بود، نقشهبرداریها و ترسیم اشکال هندسی روی خمینهها با
صفحه تخت متفاوت است و محاسبات نتایج گوناگونی دارند؛ یعنی مساحت مربع
و مثلث تغییر میکند. زوایای داخلی آنها نیز تغییر میکند و کل نقشه
برداری، نقشهکشی و محاسبات به هم میریزند.

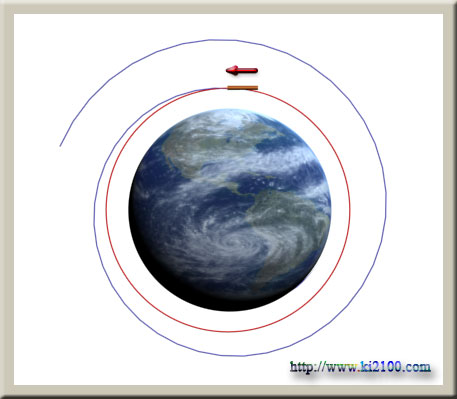
اما انیشتین طرز فکر دیگری پیدا کرد. او گفت میتوان با
پدیدههای فیزیکی متوجه شد که ما روی یک خمینه هستیم. یعنی اگر با سرعت
زیاد روی سطح خمینه حرکت کنیم، شتاب مداری یا نیروی جانب مرکز
(گریزازمرکز) گرفته و از سطح خمینه بلند شده و فاصله میگیریم. پس الان
که ما شتاب ثقل (شتاب گرانشی) زمین را احساس میکنیم داخل یک خمینه
گرانشی هستیم. یعنی تنها راه ممکن حرکت با سرعت زیاد است. اگر ما شتابی
احساس نکردیم، در خط مستقیم هستیم؛ ولی اگر به طرفی یا جهتی احساس شتاب
و نیرو کردیم، انحنایی در جهت عکس خواهد بود. الان که ما بیحرکت و
نسبت به سیاره زمین ساکن هستیم؛ ولی نیرو و شتابی را احساس میکنیم در
روی یک خم گرانشی هستیم یا همان انحنای فضا - زمان. جهت انحنا عکس جهت
نیرو یا شتاب است.
میدان تانسوری:
در ریاضیات، فیزیک و مهندسی، یک
میدان تانسوری
به هر نقطه از یک فضای ریاضیاتی، (برای نمونه فضای اقلیدسی یا یک
منیفلد) یک تانسور نسبت میدهد. میدانهای تانسوری در هندسه دیفرانسیل،
هندسه جبری، نسبیت عام، در تجزیهوتحلیل تنش و کشش در مواد و بسیاری از
کاربردهای دیگر در علوم و مهندسی به کار میروند. یک تانسور تعمیمی از
یک کمیت نردهای (مانند طول) و برداری (مانند سرعت) است. میدان تانسوری
نیز تعمیمی از میدان نردهای و میدان برداری است. تانسور عنصری هندسی
است که در ریاضی و فیزیک بهمنظور گسترش مفاهیم اسکالرها، بردارها و
ماتریسها به ابعاد بالاتر معرفی میشوند. بسیاری از ساختارهای
ریاضیاتی که به طور غیررسمی تانسور خوانده میشوند در حقیقت میدان
تانسوری هستند، مانند تانسور ریمان.
حساب تانسوری
در فیزیک نظری و زمینههای دیگر ٬معادلات دیفرانسیلی که برحسب
میدانهای تانسوری نوشته میشوند راهی بسیار کلی برای بیان روابطی که
هم ذاتاً هندسی هستند و هم در ارتباط با حساب دیفرانسیل هستند ارائه
میکنند. برای نوشتن این معادلات از نمادگذاری جدیدی به نام مشتق
هموردا استفاده میشود.
ساده
گفته باشیم ما ابزاری داریم به نام ترازو که میتوانیم در واحدهای
کیلو، پوند، اونس و... از آن استفاده کنیم. سنگ محک یا سنگ ترازوی ما
فقط فرق میکند و ترازوی دو کفه ثابت است؛ چون مثل اهرم مساوی عمل
میکند. یا واحد طول در استاندارد متر، فوت، زراع و... در هندسه
دیفرانسیل هم موجودات هندسی نسبت به یک متریک یا تانسور متریک یا میدان
تانسوری سنجیده و تحلیل میشوند و گاها روشهای ریاضی هم فرق میکنند.
در
گذشته این تانسورها علامت یا اندیسگذاری میشدند مثلاً
gu,v
که کار کمی با آنها دشوار است. نرمافزار میپل سه راهکار ارائه کرده
است. روش اندیسگذاری سابق، روش رایانهای همانند محیط ام اس داس (خط
فرمان)، روش کدنویسی در محیط جبری و تحلیلهای فیزیکی. gu,v
یا تانسور متریک یک ماتریس با ابعاد u,v است؛ یعنی ستون u و سطر v.
تانسورها در هندسه دیفرانسیل محدودیت ابعادی ندارند. یعنی میتوان یک
تانسور چندبعدی معرفی کرد. هر عضو تانسور هم خودش میتواند یک ماتریس
یا تانسور دیگری بوده باشد. یعنی اعضا یک تانسور در ظاهر ساده،
میتواند بینهایت بوده باشد و هر عضو با یک اندیس مشخص میشوند؛ یعنی
ستون و ردیف و... چندم.
روش اول و دوم برای ریاضیات محض مناسب است و
روش دوم برای فیزیک و ... فعلا به علت پیچیدگی زیاد از روش اول صرف نظر
کرده و روش دوم را معرفی میکنیم.
وقتی
که شما نرمافزار میپل را اجرا میکنید وارد محیطی همانند Command
Prompt یا PowerShell میشوید. کدنویسیها نیز شبیه برنامه C است. اما
راحت تر از متلب است. متلب هم جای خودش را دارد.

دستور اول ریست است؛ یعنی تمامی متغیرها صفر میشوند و engine (موتور
یا مولد) میپل ریستارت میشود.
در
دستور دوم کتابخانه هندسه دیفرانسیل فراخوانی میشود با کلی دستورات
آمادهبهکار.
در
دستور سوم کتابخانه تانسورها فراخوانی میشود با کلی فرامین آماده به
عمل. یعنی یک جعبه ابزار کامل ریاضی. تمامی متریک ها و تانسورها در این
کتابخانه تعریف شده هستند و خودتان هم می توانید متریک یا تانسوری
تعریف کنید.
در
دستور چهارم ما یک منیفلد (M) یا خمینه سهبعدی x,y,z تعریف کردیم و
بعد از آن به روی آن خمینه منتقل میشویم. دقت کنید که ما دیگر خارج از
خمینه نیستیم؛ بلکه به روی آن مهاجرت کردیم و از بیرون مشاهدهکردنش
دیگر بیمفهوم است. ما ماندیم با یک خمینه سوار شده بر رویش درست مثل
زین اسب.
در
دستور پنجم ما برای این خمینه یک متریک (سنجه و سنگ محک) تعریف
میکنیم.
الان
شما میتوانید راه پیموده کرده ریمان، گاوسی و انیشتین را در عرض چند
هفته یا ماه طی کنید. ۱۰ سال آنها چند ماه شماست.
فریب
و حقه رمالان و دعانویسها و نسخهنویسان و نسخه پیچان مدرن را هم
نخورید. چون از نوشتههای خود هیچ سر در نمیآورند و صرفاً مثل اسکنر،
کپیبرداری و بازگو کردهاند.

اگر
خوب دقت کنید، چیزی در مایه اسبسواری است. خمینه اول ما دوبعدی تعریف
میشود به نام صفحه. بعد ما سوار بر صفحهای دوبعدی میشویم. سپس متریک
ساده این صفحه را تعریف میکنیم. سپس به کمک تانسور دیگری به نام
تانسور انحنا تابع این انحنای صفحه را به دست میآوریم. سپس انحنای
صفحه را به دست میآوریم که صفر است. بعد از آن به خمینه کروی نقلمکان
یا مهاجرت میکنیم. اسب اول را رها کرده و سوار بر اسب دوم میشویم.
تعجب نکنید سطح کره ما دوبعدی است؛ ولی شما آن را از بیرون و در فضای
سهبعدی میبینید. ما که سوار بر کره شدیم آن را یک سطح دوبعدی
مینگریم و میپنداریم و درکش میکنیم. چشم ما فقط سطح افق را میبیند.
اینک ما یک موجود دوبعدی و در سطح دوبعدی کروی هستیم؛ ولی شما در یک
فضای سهبعدی و مشاهدهگر ما و کره هستید. اگر دوست دارید همراه ما شده
و به دنبال ما بیایید.

g متریک خمینه کروی در حالت پارامتری، U یک
تانسور میدانی است. CongruenceProperties
ویژگی های همخوانی دو خمینه یا تانسور است.
رسم توابع پارامتری شده در متلب:


رویه در متلب:


در
ابتدا یک مش گرید (صفحه تخت u,v) تعریف میکنیم. سپس تابع t را به نسبت
آن دو نوشته و رویه رسم میشود.

این
هم خود صفحه اصلی u,v است.
رسم در مختصات کروی

در
ابتدا تتا و فی را بهصورت بردار از مبدأ صفر تعریف میکنیم. بهجای
u,v یعنی صفحه تخت از آنها استفاده میکنیم. در ستر ۵ مختصات کروی را
به مختصات دکارتی تبدیل میکنیم و...
کمکم به قسمت مهم و اساسی مبحث هندسه دیفرانسیل میرسیم؛ یعنی ما یک
خمینه داریم که تابع پارامتری شده آن در دست است، متریک آن را چگونه به
دست آوریم؟ جواب خیلی ساده و راحت است. بهوسیله فرم بنیادی اول یعنی
همان اتحاد مربع دوجملهای خودمان.

این
دقیقاً به چه معناست؟
معنا و مفهوم این کدهای
ماشینی، یعنی پایان راه مار و عقرب نویسی و رمزنگاری آکادمیک یا همان
دانشگاهی. یعنی صرف انرژی و زمان ما در نهایت به نتیجهای میرسد و نه
اینکه در راه بحثهای بیهوده و بیسروته تختهسیاهی هدررفته و ایزوله
شود و البته که به جایی هم نرسند. یعنی زبان ریاضی هم برای ماشین و هم
برای انسانها مفهوم میشود و از انحصار عدهای دانشگاهی خاص خارج
میشود که نه خودشان و نه دیگران هیچچیزی از گفتههایشان سر در
نمیآورد. یعنی ریاضی هم برای خود آزمایشگاه پیدا میکند. هرکسی ادعای
دارد، باید حرف و نظر خود را در این آزمایشگاه به ثبوت برساند. گذشت
زمان آزمونهای فکری و مدلهای ریاضی مندرآوردی. اینک نهتنها
آزمونهای فیزیکی باید انجام شوند؛ بلکه نظریات ریاضی نیز باید ماشینی
شوند تا خطاها و اشتباهات حتی منطق غلط آنها آشکار و رویت شوند.
چون
خیلیها فکر میکنند که ریاضیات آخر منطق است و هر کسی چند خط معادله
ریاضی نوشت، حتماً آدمی منطقی با منطق درست است. غافل از اینکه ممکن
است کل منطقش اشتباه بوده و تمامی محاسبات و روابط غلط و غیرقابلتحقق
یا اجرا بوده باشند. دنیا عوض شده هر نظریه و رابطه ریاضی شما اولاً
باید قابلفهم توسط دیگران و ماشین بوده باشد ثانیاً به جوابی درست و
کارآمد و مفیدی برسد. وگرنه باطل است هرچند که ریاضی بوده باشد.

یعنی
در دنیای ما با اینجور چیزها دیگرکسی نمیتواند برای خودش به دنبال
کسب شهرت و ثروت و تأسیس دکان، سوپرمارکت، هایپرمارکت و... مدرن بوده
باشد و صدالبته عوامفریبی و گنده یا گزافهگویی. محصلین دبیرستانی
خیلی سریع میتوانند مطالب او را تجزیهوتحلیل یا آنالیز کنند و در
نهایت بگویند که درست گفتی یا اینکه چرند گفتی. به طور مثال نمادهای
کریستوفل، تانسور انحنا و وارون خمینه کروی، خیلی سریع و البته بدون
خطا به دست میآیند تا...
انحنای ژئودزینک یک دایره عرض جغرافیایی بر کره:
این انحنای ژئودزینک را با
استفاده مستقیم از تعریف قراردادی برای زاویه تتا پیدا میکنیم. بردار
انحنای K در صفحه دایره قرار دارد و طولش مساوی عکس شعاع این دایره
است. یعنی:


مشتق هموردا (کواریانت)

عملگر انتگرال، مشتق و حد روی متریک و تانسورها.

یک
روش دیگر برای انتگرالگیری

d به
معنی فاصله distance و D به معنی دیفرانسیل یا همان مشتق است.

دیورژانس

تمام محاسبات در DifferentialGeometry با استفاده از دستور DGsetup
برای مقداردهی اولیه محیط محاسباتی شروع می شود. یعنی تعریف منیفلد
اصلی یا متریک آن.
از +/- برای جمع و تفریق، * برای ضرب اسکالر (داخلی)، &t برای ضرب
تانسور (خارجی) و &w برای ضرب گوه ای wedge product استفاده کنید.
در اینجا شکل معمولی برای متریک ثابت (مستقل از زمان) ثابت چرخشی است
که به عنوان آنساتز شروع برای حل معادلات اینشتین استفاده می شود.
دو تابع "A(r)"
و "B(r)"
با معادلات انیشتین مشخص خواهد شد.
دستور DGinfo یک برنامه کاربردی است که می تواند برای به دست آوردن
اطلاعات در مورد محیط محاسباتی و اطلاعات مربوط به اشیاء مختلف
DifferentialGeometry استفاده شود.
در اینجا ما از DGinfoto تمام ضرایب تانسور انیشتین را استخراج می
کنیم.

اکنون از دستور Maple pdsolve برای ادغام این معادلات دیفرانسیل
استفاده می کنیم:
ثابت _C1 اساساً جرم منبع نقطه ای میدان گرانشی است.
ثابت _C2 به راحتی با مقیاس مجدد زمان به -1 نرمال می شود.
این متریک شوارتزشیلد در مختصات استاندارد است.
تانسور اینشتین در صورت لزوم ناپدید (صفر) می شود.
مسلماً این متریک یک چهار بردار است.
اعمال تغییرات جبری در تانسورها
متریک یا تنسور معکوس:

تعریفکردن تانسور رتبه ۳ . پایین آوردن شاخص دوم T .
افزایشدادن شاخصهای (۱ و 3) T با استفاده از متریک معکوس، "h" .
دوباره مرتبکردن شاخصهای ۱ و ۲.

التصاق آفین
در هندسه دیفرانسیل،
التصاق آفین
(Affine Connection)، [الف] شیئی هندسی روی منیفلدهای هموار است که
فضاهای مماس مجاور را به هم متصل میکند. [ب] بنابراین این ابزار امکان
دیفرانسیلگیری از میدانهای برداری مماس را میدهد، بهگونهای که
همچون توابعی روی منیفلدها عمل میکنند که مقادیر خروجیشان در فضای
برداری ثابت و فیکس شدهای قرار دارند. الصاقها جزو سادهترین روشهای
تعریف دیفرانسیل روی مقاطع کلافهای برداریاند.

یک
التصاق آفین روی کره، صفحه مماس آفین را از یک نقطهبهنقطه دیگر
میغلتاند. طی این عملیات، نقطه تماس صفحه مماس با کره، اثر یک منحنی
را بر روی کره برجای میگذارد. به این عمل در هندسه دیفرانسیل پیشروی
(development) گویند.
مشتقات:
میتوان مشتق بیرونی یک
شکل دیفرانسیل، مشتق لی هر میدان تانسوری را باتوجهبه یک میدان برداری
یا مشتق کوواریانت هر میدان تانسوری را باتوجهبه یک اتصال محاسبه کرد.
تعریف یک منیفلد و مشتق بیرونی آن. تعریف یک میدان برداری X و یک
تانسور T و محاسبه مشتق Lie. تعریف یک اتصال و مشتق کوواریانس آن.

مشتق لی
در ریاضیات ٬
مشتق لی
که بهافتخار سوفوس لی نامگذاری شده است٬ تغییر یک میدان تانسوری (در
حالت کلی٬شامل میدان نردهای و میدان برداری و یک - فرم) را در جهت یک
شارش یک میدان برداری دیگر به دست میدهد. این تغییر در دستگاهها
مختصات مختلف ناوردا است و به همین دلیل مشتق لی بر روی هر منیفلد
دیفرانسیل پذیر تعریف میشود.
ایجاد تانسورهای متقارن
بهدستآوردن
اجزای هر تانسور باتوجهبه هر پایهای با دستور GetComponents

تانسورهای انحنا:
تانسور انحنای ریمان، تانسور ریچی، اسکالر ریچی و تانسور ویل یک متریک
به راحتی محاسبه می شوند.
در اینجا از متریک گودل استفاده می کنیم.

کار با تترادهای Orthonormal
بسیاری از محاسبات در نسبیت عام را میتوان با تعریف یک تتراد متعامد و
با بیان متریک و تمام تانسورهای دیگر بر حسب این تتراد متعارف به طور
چشمگیری ساده کرد. این امر بهویژه زمانی صادق است که بتوان یک هم فریم
را با معادلات ساختاری ساده انتخاب کرد. یک تصویر ساده از این با متریک
گودل از مثال قبلی ارائه میشود.

کار با نول تتراد و فرمالیسم نیومن-پنروز بسته هندسه دیفرانسیل از
محاسبات در تمام فرمالیسم های مختلف برای نسبیت عام پشتیبانی می کند -
محاسبات مختصات، تترادهای متعارف، تترادهای تهی و فرمالیسم
نیومن-پنروز، و فرمالیسم اسپینور دو جزء.
ابزارها برای حرکت از یک فرمالیسم به فرمالیسم دیگر به راحتی در دسترس
هستند. در این مثال ما اسکالرهای انحنای نیومن-پنروز را برای یک متریک
محاسبه می کنیم.
کار با نول تتراد و فرمالیسم نیومن - پنروز
بسته هندسه دیفرانسیل از محاسبات در تمام فرمالیسمهای مختلف
برای نسبیت عام پشتیبانی میکند - محاسبات مختصات، تترادهای متعارف،
تترادهای تهی و فرمالیسم نیومن - پنروز، و فرمالیسم اسپینور دو جزء.
ابزارها برای حرکت از یک فرمالیسم به فرمالیسم دیگر بهراحتی در دسترس
هستند. در این مثال ما اسکالرهای انحنای نیومن - پنروز را برای یک
متریک محاسبه میکنیم.
دستور DGGramSchmidt و NullTetrad ابزارهای مفیدی را برای ساخت
تترادهای تهی ارائه می کنند.
در اینجا موردی است که برای این مثال استفاده خواهیم کرد
در اینجا اسکالرهای انحنای نیومن-پنروز برای این تتراد صفر آمده است.

فرمالیسم اسپینور دو جزء به عنوان یک تصویر سریع از فرمالیسم اسپینور 2
جزء، ما اسپینور Weyl را برای متریک از پاراگراف قبل محاسبه می کنیم.
برای کار با اسپینورها از DGsetup برای تعیین مختصات فضا-زمان و همچنین
مختصاتی که برای اسپینورها و مزدوج های پیچیده آنها استفاده می شود
استفاده می کنیم.

همخوانی ها همخوانی های خط (به ویژه همخوانی های تهی) نقش مهمی در
تحلیل هندسی فضا-زمان ایفا می کنند.
ما به متریک مثال قبلی ادامه می دهیم.
ما نشان میدهیم که همخوانی تعریفشده توسط D_ris یک جهت تهی اصلی بدون
برش را تعریف میکند.

فضا - زمان الکترو خلا
اگر میدان الکترومغناطیسی
وجود داشته باشد که معادلات میدان انیشتین - مکسول را حل کند،
فضا-زمان، فضا-زمان الکترو-واک نامیده می شود. با استفاده از دستور
RainichConditions و RainichElectromagneticField می توان مشکل تصمیم
گیری در مورد اینکه آیا فضا-زمان الکترو-واک است یا خیر را حل کرد. در
اینجا یک مثال ساده ارائه می شود.

چرا اساسیترین چیز در هندسه دیفرانسیل متریک است؟
برای اینکه یک مختصات دکارتی دوبعدی یک یا چهار عدد مربع است. مختصات
دکارتی چهاربعدی یک یا هشت مکعب است. مختصات قطبی یک دایره و مختصات
کروی یک کره و مختصات استوانهای خود استوانه است. در هندسه دیفرانسیل
هم متریک در واقع همان مختصات است. یعنی ما بینهایت دستگاه مختصات و
شکل یا رویه یا حجم یا خمینه داریم. در هندسه دیفرانسیل هر موجود هندسی
و فیزیکی برای خودش مختصات و متریکی دارد.
در
حقیقت بعضی از این تانسورها کار مقایسه متریکها و دستگاههای مختصات
را با یکدیگر دارند. یعنی مثلاً کره به نسبت دستگاه دکارتی چقدر انحنا
و... دارد.
ولی
هندسه دیفرانسیل بسیاری از تعاریف قراردادی و توافقی دارد و خیلی از
نتایج بهصورت تجربی کسب شده و فعلاً هیچگونه توجیه و اثبات ریاضی هم
ندارند؛ ولی کاربردهای مهمی پیدا کردهاند.
تمام
جلسات DifferentialGeometry با اجرای دستور DGsetup شروع میشوند. این
دستور برای راهاندازی محیط محاسباتی با ایجاد سیستمهای مختصات،
فریمها، جبرهای لی و غیره استفاده میشود. دستور DGsetup را میتوان
چندین بار در یک جلسه Maple معین استفاده کرد.
ما
ابتدا از DGsetup برای ایجاد یک سیستم مختصات برای یک منیفولد ۲ بعدی
استفاده میکنیم. ما [x, y] را بهعنوان نام مختصات اعلام میکنیم و
منیفولد (یا به طور دقیقتر، وصله مختصات منیفولد) را E2 مینامیم.
در این مرحله، نام مختصات محافظت شده است و نمیتوان مقادیری
را به آنها اختصاص داد. بردارهای D_x، D_y اختصاصدادهشده و محافظت
میشوند. آنها مبنای مختصات فضای مماس E2 را در هر نقطه [x, y] تعریف
میکنند.
دیفرانسیل:
۱-شکل dx و dy اختصاصدادهشده و محافظت میشود. آنها مبنای
مختصاتی را برای فضای کتانژانت E2 در هر نقطه [x, y] تعریف میکنند. در
درس بعدی به عملیات پایه شامل بردارها، فرمها و تانسورها خواهیم
پرداخت. قبل از ادامه، متذکر میشویم که تمام اجسام هندسی مختلف که در
هندسه دیفرانسیل به وجود میآیند، یک نمایش داخلی در Maple دارند که
ویژگیهای مختلف جسم و همچنین تمام مقادیر اجزای جسم هندسی را توصیف
میکند. درک دقیق این نمایش داخلی برای استفاده از هیچ یک از دستورات
DifferentialGeometry لازم نیست - در اینجا ما بهسادگی میخواهیم
کاربر را از وجود آن آگاه کنیم. برای نمایش داخلی فیلد برداری D_x و
1-form dy، از دستور Maple lprint استفاده کنید.

توجه داشته باشید که نمایش داخلی D_x به وضوح D_x را به عنوان یک شی
هندسی از نوع "بردار" متصل به منیفولد E2 مشخص می کند، در حالی که
نمایش داخلی dy نشان می دهد که dy یک "فرم" متصل به منیفولد E2 است و
دارای درجه 1 است.
برای
ایجاد یک دسته فایبر (رشته) رتبه 2 روی یک منیفولد F پایه سهبعدی با
مختصات پایه [x, y, z] و مختصات رشته [u, v]، از دستور DGsetup بهصورت
زیر استفاده کنید:

توجه
داشته باشید که اعلان Maple به F تغییر کرده است. در محیط
DifferentialGeometry، اعلان Maple به نام سیستم مختصات فعلی یا فعال
تغییر میکند. نام اعلان همیشه نام سیستم مختصات یا منیفولد آخرین شیء
محاسبه شده را منعکس میکند.
برای ایجاد فضای جت مرتبه دوم J^2 (R^2, R) با متغیرهای مستقل [x, y] و
متغیر وابسته [u]، از دستور DGsetup با نحو زیر استفاده کنید:

در این زمینه، متغیر وابسته u اکنون به عنوان u[ ]، مشتق u نسبت به x
u[1]، مشتق u نسبت به y u[2]، مشتق دوم u است.
نسبت به x برابر با u[1,1] و غیره است. برای از بین بردن نمایش
متغیرهای محافظت شده، فیلدهای برداری و فرم های 1 دیفرانسیل، DGsetup
را با گزینه quiet اجرا کنید.

نرمافزار میپل یک سیستم جامع help یا کمک دارد که میتوانید به بخش
مربوطه مراجعه و با دستورات آن آشنا شوید. کل مطالب مربوط به ریاضیات
در این مجموعه گردآوریشده است. مراجعه به آن و انجامدادن تمرینات
بهمراتب بهتر و مفیدتر از کتب ریاضی و فیزیک است.
ایجاد دو ماتریس و ضرب اسکالر (داخلی) و ضرب خارجی (برداری) و جمع آنها
همچنین ضرب گوه ای.


تبدیل متریک (ضرب گوهای) به یک تنسور. ایجاد یک آرایه. مقداردهی به
آرایه بهازای هر اندیس. کپی اندیس.

اگر
دقت کنید مقداردهی سهبعدی است؛ ولی فقط دو بعد آرایه دیده میشود.
اگر یک جمعبندی کلی داشته باشیم، عملگرهای دیفرانسیل در حساب و جبر
کاربردهای خاصی برای خودشان دارند. ولی در هندسه دیفرانسیل معادلات
پارامتری شده و مفهوم عملگرهای دیفرانسیل تغییر پیدا میکنند. به طور
مثال خط و صفحه مماس دیگر غیرقابلدسترس میشوند. تمامی سعی و تلاشها
منجر به یک خم یا خمینه میشوند. بعداً مجبوریم دستگاههای مختصات را
تغییر دهیم و متریکها را وضع کنیم. مشکل زمانی حاد میشود که نور
خاصیت سهبعدی دارد و چشم و مغز ما فقط موجودات سهبعدی را رویت و
تحلیل میکنند. ولی امکان فرمولبندی و مدلسازی موجودات چندبعدی مقدور
میشود. در نهایت مجبوریم عملگرهای تانسوری را وضع کنیم تا موجودات
چندبعدی در فضای سهبعدی دکارتی مقایسه و تحلیل شوند. یعنی چندین
دستگاه مختصاتی و متریک گوناگون با ابعاد متنوع تودرتو. ساده گفته
باشیم اگر غفلت کنید دچار ضایعات جبرانناپذیر بینایی و مغزی میشوید.
چون وارد دنیایی شدهاید که چشم قادر به دیدن و مغز قابلیت تحلیل را
ندارد. همه چیز با اعداد و ارقام است و نه بهصورت استدراکی با حواس
پنجگانه.
به تعاریف و قراردادها نیز باید دقت کنید. کره در فضای دکارتی موجودی
سهبعدی است؛ ولی در هندسه دیفرانسیل سطح آن دوبعدی است. تعریف ابعاد
میتواند دور از انتظارات سابق ما بوده باشد.
آسیب مغزی، ضربه
یا تروما، تومور، انگل، اختلالات عصبی و هورمونی، نقص یا تغییرات مغزی
مادرزادی، اختلاف در ساختار چشم و عصب بینایی، تحتتأثیر دارو یا مواد
شیمیایی بودن میتواند باعث تغییر در احساسات و حواس پنجگانه و
استدراک محیطی شود. ازاینرو بعضی ریاضیدانان و فیزیکدانان ممکن است
نظریات عجیبوغریبی ارائه کنند که توسط دیگران قابلدرک یا پذیرش هم
نبوده باشد حتی مدلسازی و فرمولبندی هم شده باشند. بههرحال دلیل فوت
انیشتین کاملاً مشخص نبود و نیاز به کالبدشکافی داشت. خیلیها نیز
کنجکاو بودند که درون مغز او چه خبر است. ولی مغز او ناپدید شده و به
سرقت رفت و بعداً تکههایی از آن را به دیگران ارائه کردند که مشخص
نیست واقعاً مغز چه کسی است؛ چون تست دیانای نشده و نمیتواند که
بشود؛ چون جنازه او سوزانده شد و چیز زیادی از بستگان نزدیک او در
دسترس نیست و مغز او به فرمالین، الکل و... آلوده شده است.
ریاضیات و هندسه پیشرفته چیست؟
انسان برای حرکت از دو پا استفاده کرده و بعداً از حیوانات
چهاردستوپا. ولی بعداً چرخ را اختراع و گاری و درشکه ساخته است. بعدها
اسب و... حذف و دیگ بخار و موتور درونسوز جای آن را گرفته است و هم
اینک باطری و...
در ابتدا عملیات دیفرانسیل روی چند متغیر خطی
بوده است. بعدها روی توابع مثلثاتی و زاویه. با پیشرفت بیشتر
پارامترهای خطی حذف و عملیات دیفرانسیل روی یک یا چند زاویه بر حسب
رادیان صورتگرفته است. چرا؟
برای اینکه روی منحنیها، خمها و
خمینهها یعنی اشکال و موجودات مدور کار میکردند. چون دنیای پیرامونی
ما و فیزیک اینگونه است. نسبیت خاص روی گذر چیزی به نام زمان متمرکز
بوده است. یعنی زمان دامنه توابع محسوب میشده است. این زمان خطی است
یا چیزی شبیه زاویه؟
جواب هیچکدام است؛ چون زمان قابل مشاهد نیست؛
یعنی موجودی فیزیکی نیست. جریان وقتی عجیب شده که نسبیت عام از هندسه
دیفرانسیل استفاده کرده است و بجای دامنه اصلی زاویه، از زمان استفاده
کرده است. قبلاً ریمان متوجه شده بود که وقتی ما معادله اشکال سهبعدی
را پارامتری و تبدیل به متریک میکنیم یک بعد کاهش داریم. معادله
پارامتری شده کره سهجزئی است (سهبعدی دکارتی)؛ ولی متریک آن دوجزئی
(دوبعدی تانسوری) میشود. ریمان ازاینرو جا برای ابعاد بیشتر پیدا کرد
و متریک های سهجزئی (سه اندیس) را ارائه نمود. اما انیشتین واقعاً
دستبهکار عجیبی زده است؛ چون گذر زمان نه خطی و نه دورانی یا چرخشی
(زاویهای) است و برای همگان سؤال این است که خمینههای انیشتین چه
شکلی هستند؟ آیا او دچار یک خطای اساسی و بنیادی شده است؟
تانسورهای
انیشتین چهار اندیس دارند و اگر به معادلات دکارتی تبدیل شوند ۵ بعدی
خواهند شد. یعنی یک افزایش در بعد. جریان وقتی غامض میشود که زمان در
یک اندیس بعد است؛ ولی در اندیس دیگر دامنه تابع بعد دیگر تعریف شده
است. درگیری چرخ و نعل اسب هم همیشه مشهود است. یعنی عملیات دیفرانسیل
هم بر روی زاویه است و هم بر روی ابعاد. زمان گاهی دامنه است و گاهی
برد.
کاربرد اول دیفرانسیل تحلیل داده و ارقام بود؛ اما بعداً در مورد تحلیل
اشیا و اجسام کاربرد پیدا کرد. آیا انیشتین سعی کرده داده و ارقام را
وارد اشیا و موجودات فیزیکی کند؟ آیا متوجه اصل قضیه دیفرانسیل و
کاربرد آن نبوده است؟ یعنی فرق موجود فیزیکال و آمار را نمیدانسته
است.
بدترین نوع و مدل شروع مطالعه و فراگیری هندسه دیفرانسیل، داشتن نگرش
هندسه تحلیلی، جبری یا حتی مکانیکی است. یعنی فکر کنیم یک خم معادله
حرکت، سرعت و شتاب و... است. درحالیکه بهترین نوع و مدل شروع مطالعه و
فراگیری هندسه دیفرانسیل، داشتن نگرش فیزیکال خم یا رویه بهعنوان یک
موجود مستقل فیزیکی است که درون آن هیچگونه اطلاعات و آماری وجود
ندارد.
محمدرضا طباطبايی ۱۴۰۳/۰۴/
۱۷
http://www.ki2100.com

