فاصله از مركز مدارها در شكل توسعه يافته ستاره داوود
مدار اول
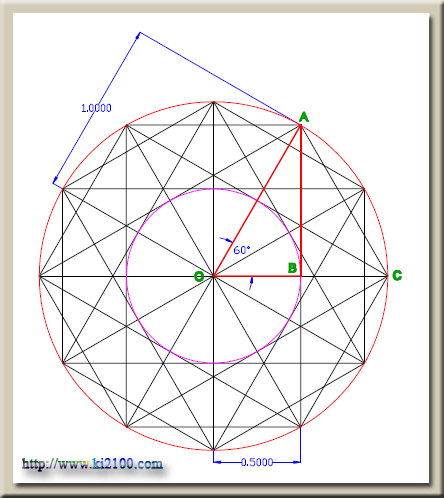
در دايره مثلثاتي فوق كمان
AC برابر است با 2*(12/360) يا 6/360 يعني 60 درجه ، با
توجه به اينكه در
مثلث قائمالزاويه OAB زاويه
BOA برابر 60 درجه است ، ضلع
OB برابر خواهد بود با
OAcos60° يا r/2 يعني
0.5=2/1 .
مدار دوم
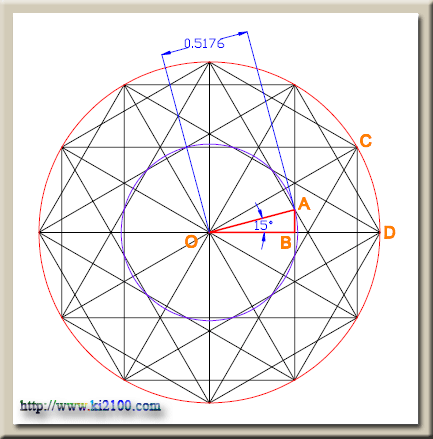
در مثلث قائمالزاويه
OAB زاويه AOB=15° ميباشد براي اينكه پاره خط AO نيمساز
زاويه COD بوده و كمان
CD برابر 30 درجه ميباشد و همچنين OB=r/2 ميباشد . با توجه به اينكه OB=OAcos15° پس
OA=OB/cos15°=(r/2)/cos15°→OA=r/2cos15°=r/[2(√6+√2)/4]=2r/(√6+√2)=
2r(√6-√2)/(√6+√2)(√6-√2)=2(√6r-√2r)/6-2=(√6r-√2r)/2=(√6-√2)/2
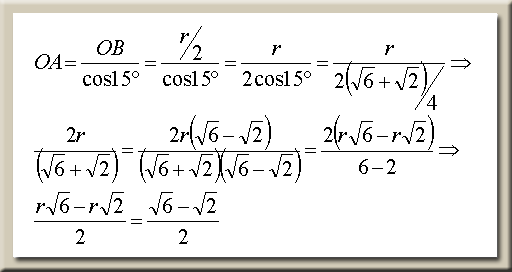
مدار سوم
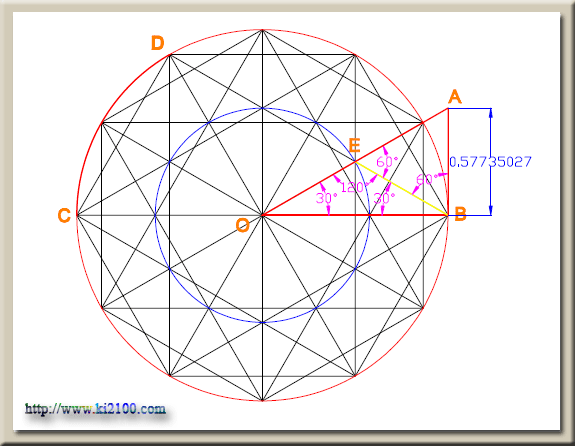
با توجه به اينكه كمان
CD برابر 60 درجه ميباشد ، زاويه
CBD برابر با نصف CD
يعني 30 درجه خواهد بود . در اين صورت زاويه
OEB برابر 120 درجه و زاويه BEA
برابر 60 درجه و زاويه EBA نيز برابر 60
درجه ميباشد . در اين وضعيت مثلث EBA
متساويالاضلاع بوده و AB=EB ميباشد و با
در نظر گرفتن اينكه مثلث OEB متساويالساقين
است EB=EO بوده و EO=AB
خواهد شد و چون AB برابر
r*tan30° ميباشد در نتيجه
OE يا شعاع مدار سوم نيز برابر r*tan30° يا
r√3)/3)
و 3/3√ خواهد شد .
مدار چهارم
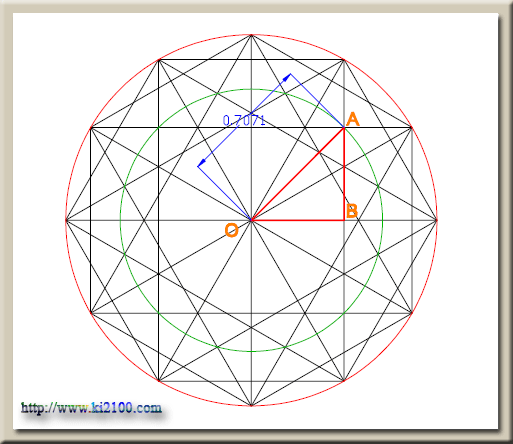
در مثلث
قائمالزاويه OAB دو ضلع
OB و BA مساوي يكديگر بوده و اندازه
هر دو برابر r/2 ميباشد .
OA²=OB²+BA²→OA²=2(r/2)²→OA=√2(r/2) = r√2/2=√2/2
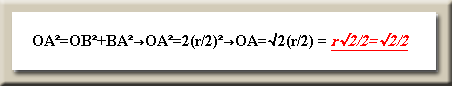
مدار پنجم
در مثلث
قائمالزاويه OAB
اندازه ضلع OB برابر است با OAcos30° يعني
r√3/2
يا 2/3√ .
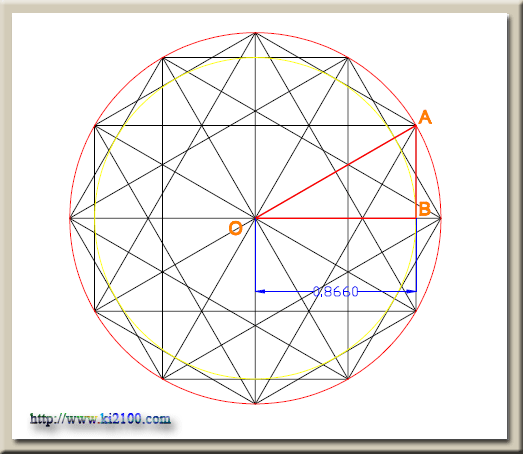
مدار ششم
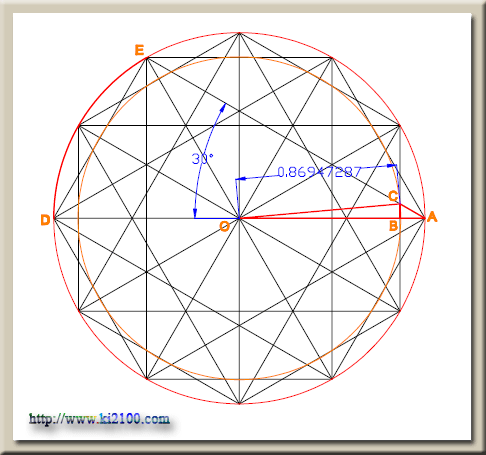
در مثلث قائمالزاويه
ABC زاويه BAC
روبروي كمان DE برابر 30 درجه ميباشد .
AB=r-r√3/2=(2r-r√3)/2
BC/BA=tan30°→BC/[(2r-r√3)/2]=(√3/3)→3BC=√3(2r-r√3)/2=(2√3r-3r)/2→
6BC=2√3r-3r→BC=(2√3r-3r)/6
و در مثلث قائمالزاويه OBC :
OB²+BC²=OC²→(r√3/2)²+[(2√3r-3r)/6]²=OC²;(r√3/2)²=3r²/4&
[(2√3r-3r)/6]²=[(2√3r)²-2(2√3r)(3r)+(3r)²]/36=(12r²-12√3r²+9r²)/36→
(21r²-12√3r²)/36;
3r²/4+(21r²-12√3r²)/36=(27r²+21r²-12√3r²)/36=(48r²-12√3r²)/36→
[12(4r²-√3r²)]/36=(4r²-√3r²)/3=OC²→OC=√[(4r²-√3r²)/3]=√[(4-√3)/3]
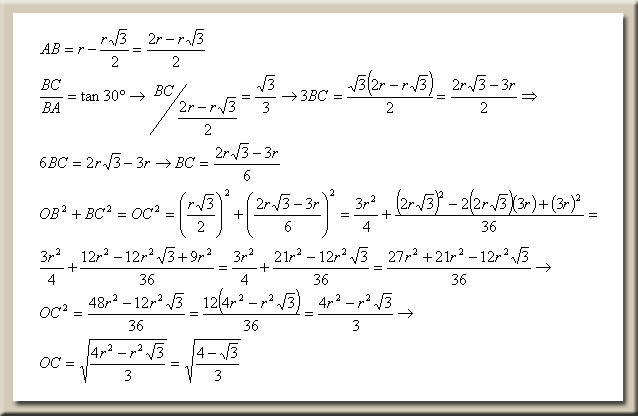
مدار هفتم
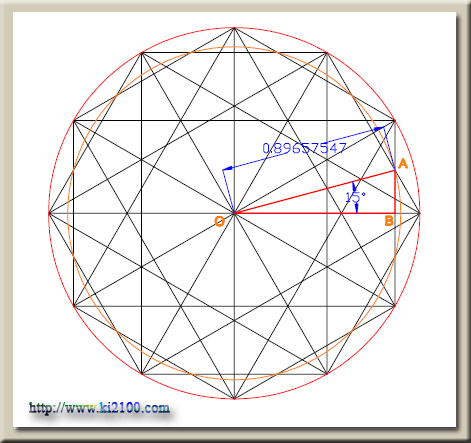
در مثلث قائمالزاويه
OAB ضلع OB برابر
است با r√3/2
OB=OAcos15°→OA=OB/cos15°→OA=(r√3/2)/cos15°=r√3/2cos15°=
r√3/[2(√6+√2)/4]=2r√3/(√6+√2)=2r√3(√6-√2)/(√6+√2)(√6-√2)=
2(r√18-r√6)/6-2=(r√18-r√6)/2=r√6(√3-1)/2=√6(√3-1)/2
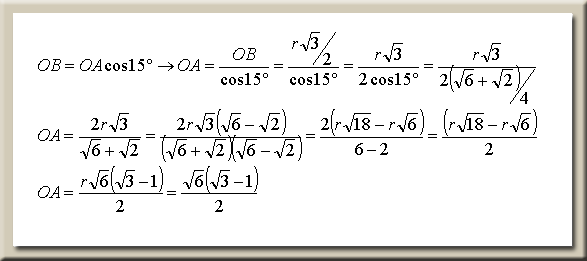
مدار هشتم
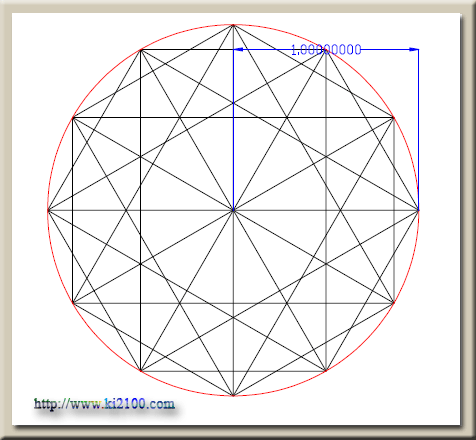
در كليه محاسبات
فوق مقدار r را يك واحد در نظر گرفتهايم .
لازم به توضيح است
، همانطور كه از برآورد اندازههاي فوق بر ميآيد ، اعداد 1 ، 2 ، 3 ،
4 ، 6 ، 8 ، 9 ، 12 ،18 ، 36 ، 48 كاربرد داشتهاند و اين اعداد مربوط
به سيستم شمارش اعداد بر مبناي دوازدهتايي يا حساب دوجيني ميباشد براي اينكه :

|
عدد بر مبناي دوازدهتايي |
تقسيمات |
عدد بر مبناي دهتايي |
|
10 |
1=12/12 |
12 |
|
30 |
3=12/36 |
36 |
|
40 |
4=12/48 |
48 |
|
16 |
12 + 6 = 18 |
18 |
و همچنين زاويههاي 30
، 60 ، 90 و
15
درجه كاربرد داشتهاند و همانطور كه ميدانيم اندازه گيري ابعاد در
هندسه و مثلثات با استفاده از اين زاويهها بسيار سهل و آسان و كار آمد
بوده و مربوط به تقسيمات دوجيني دايره ميشود و نسبتهاي مثلثاتي اين زاويهها به راحتي از رابطه فيثاغورس محاسبه ميشوند . در واقع اشكال و اعداد و ارقام فوق اشاره به
نوعي هندسه دارد كه ميتوان نام آن را هندسه دوجيني ناميد
كه تا به امروز موفقيتهاي بسياري را در زمينه رياضيات و ساير علوم به همراه داشته
است ، البته اين در حالي است كه از اين زوايا در مبناي دهتايي استفاده
شده است .
جدول
فاصله از مركز مدارها در شكل توسعه يافته ستاره داوود
:

|
شعاع مدارها |
r=1 |
مقدار عددي در
محاسبات |
|
1 |
r/2 |
1/2 |
.5 |
|
2 |
(√6r-√2r)/2 |
(√6-√2)/2 |
.517638 |
|
3 |
r√3/3 |
√3/3 |
.577350 |
|
4 |
r√2/2 |
√2/2 |
.707106 |
|
5 |
r√3/2 |
√3/2 |
.866025 |
|
6 |
√[(4r²-√3r²)/3] |
√[(4-√3)/3] |
.869472 |
|
7 |
r√6(√3-1)/2 |
√6(√3-1)/2 |
.896575 |
|
8 |
r |
1 |
1 |
محمدرضا طباطبايي 22/8/86
http://www.ki2100.com