تحلیل معادله شرودینگر در مختصات
دوبعدی دکارتی و موهومی
همانطور که میدانیم معادله شرودینگر معادلهای است که سعی
میکند چگونگی تغییر حالت کوانتومی یک سامانه فیزیکی، نسبت به زمان را
توصیف کند. معادلات مستقل از زمانش سعی میکند که احتمال حضور ذرات در
مکانهای مشخص را تعیین کند و چنین به نظر میرسد که فعلاً یکی از
معادلات بسیار مهم در مکانیک کوانتوم است. اینک ما سعی میکنیم که این
معادله دیفرانسیل (مشتق مرتبه دوم) را برای یک ذره در یک مختصات دوبعدی
دکارتی حل کنیم. ابعاد مدنظر ما (جعبه) مستطیل
L
در L
بسته و باز است. برای حل، دو شرایط مرزی در نظر گرفته شده است. یعنی
conds1
و conds2
. لاپلاسین
در
مختصات دکارتی نوشته شده است. تابع موج
f(x,y)
است.

در شرایط مرزی
conds1
چنین به نظر میرسد که معادله خوب عمل کرده است. زیرا مستطیل (جعبه) از
چهار طرف بسته و محدود شده است (هم محور
x
و هم y) و ذره راهی برای فرار و گریز ندارد و معادله در بازه صفر تا
L
برای
y
حل شده است. مقدار
n
از عدد یک شروع شده و مقادیر تابعیت برای
x
و y
سینوسی کسینوسی (مثلثاتی) است.
ولی در شرایط مرزی
conds2
چنین به نظر میرسد که معادله خوب عملنکرده است. زیرا مستطیل (جعبه)
فقط از دو طرف بسته و محدود شده است . ولی دو طرف باز یا نامحدود دارد
(از طرف محور
x
باز و نامحدود است). یعنی ذره میتواند از دو طرف بگریزد و فرار کند.
ولی معادله در بازههای بالا و پایین صفر برای
L
جواب دارد! (جواب برای ذرهای که وجود ندارد یا خارج از محدوده است)
مقدار n
از عدد صفر شروع شده و مقادیر تابعیت برای
y
مثلثاتی ولی برای
x
نمایی است. ولی معادله برای مقدار صفر برای
y
خوب عمل کرده است. اینک این سؤال مطرح میشود که راهکار برای حل این
مشکل چیست؟
به باور ما معادله میبایست به مختصات موهومی دوبعدی منتقل
شود. این کار با ضرب
i
به محور
y
انجام میشود.

مشکل حل شده است. معادله در شرایط مرزی
conds2
در بازههای بالا و پایین صفر برای
L
جواب ندارد و با قطعیت صفر است! چون اولاً ذره گریخته و وجود ندارد و
یا اینکه خارج از محدوده (شرایط مرزی) است و معادله در شرایط مرزی
conds1
در بازه صفر تا L
برای y
حل شده است. جواب بهصورت یک عدد مختلط خواهد بود و 1/2 و
i/2
اشاره به همان انرژیهای جنبشی و نسبیتی در
مباحث قبلی دارد. به بیان ساده معادلات کوانتومی برای شرایط مرزی بسته
و محدود شده کارایی دارند و در شرایط مرزی باز و نامحدود هیچ جوابی
ندارند. به طور مثال ذره نوترون درون یک هسته یا یک ستاره نوترونی و
سیاهچاله تعریف دارد و خارج از آن شرایط مرزی، عمر متوسط آن ۹۱۸ ثانیه
است و به پروتون، الکترون و پادنوترینو واپاشیده میشود و بهتر است
معادلات کوانتومی در مختصات موهومی توسعه پیدا کند تا به قطعیت برسد.
در حقیقت شرودینگر همیشه گربه را در داخل یک جعبه دربسته فرض میکرد،
ولی ما آن گربه را در یک تونل
دودرهباز و نامحدود و حتی بیرون آن
تصور کردیم.

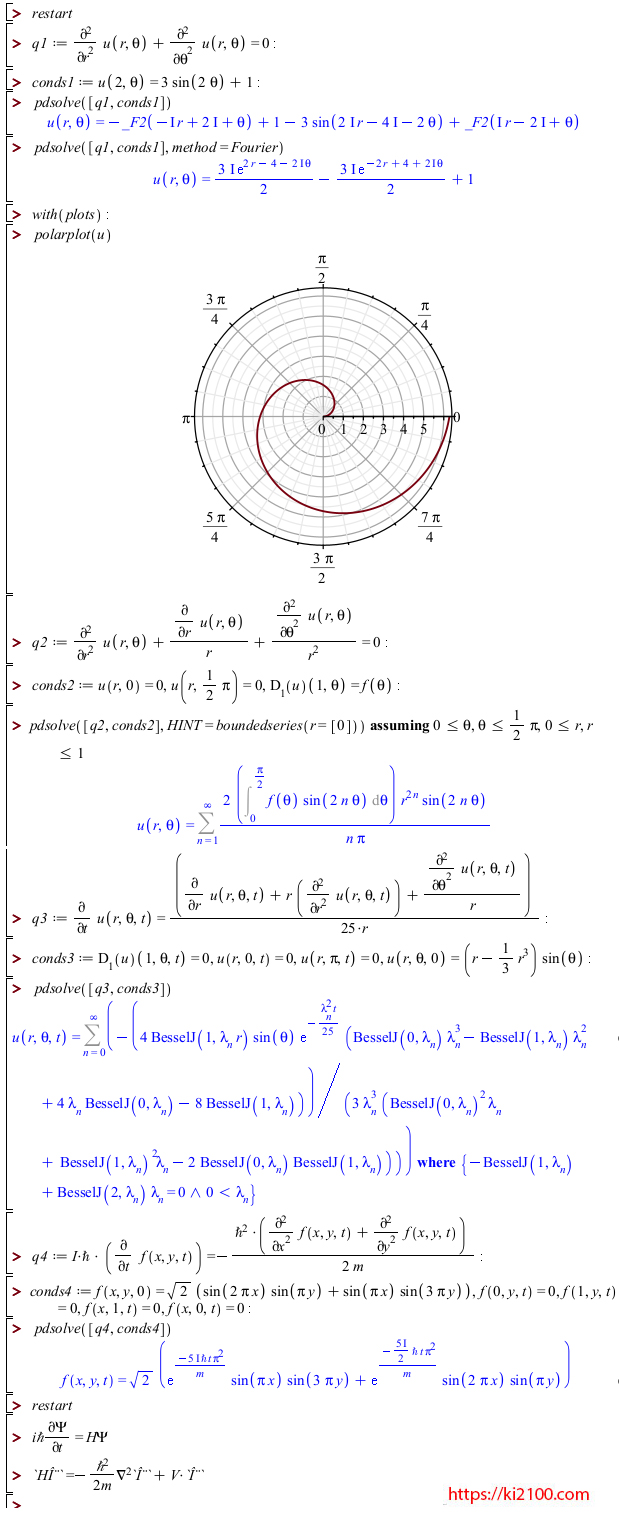
ترسیمات:
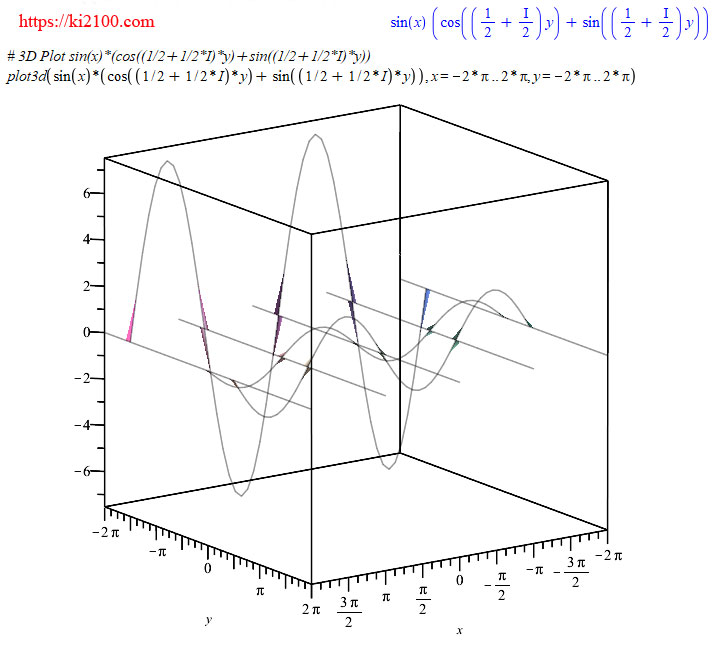
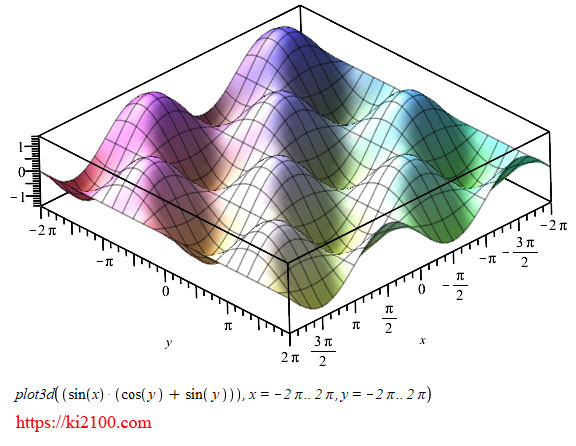
تحلیلهای اولیه و ابتدایی میتواند اینگونه باشد که چهار ۱-
میدان واحد کوانتومی، ۲- میدان الکتریکی، ۳- میدان موهومی مغناطیسی و
۴- میدان گرانشی توسط یک شبکه بههمپیوسته و ماتریس فوق را تشکیل
دادهاند.
ترسیم در مختصات موهومی سهبعدی:
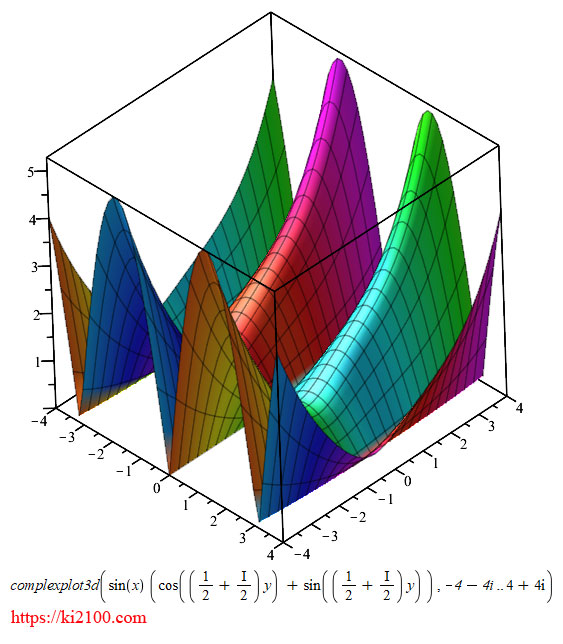
اگر مقادیر x و y را برابر فرض کنیم، در
مختصات موهومی دوبعدی:
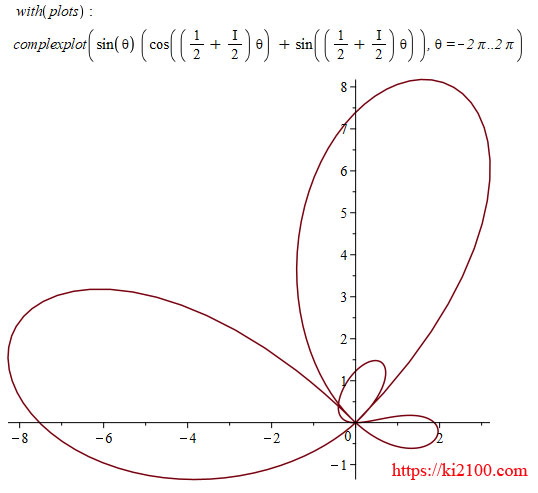
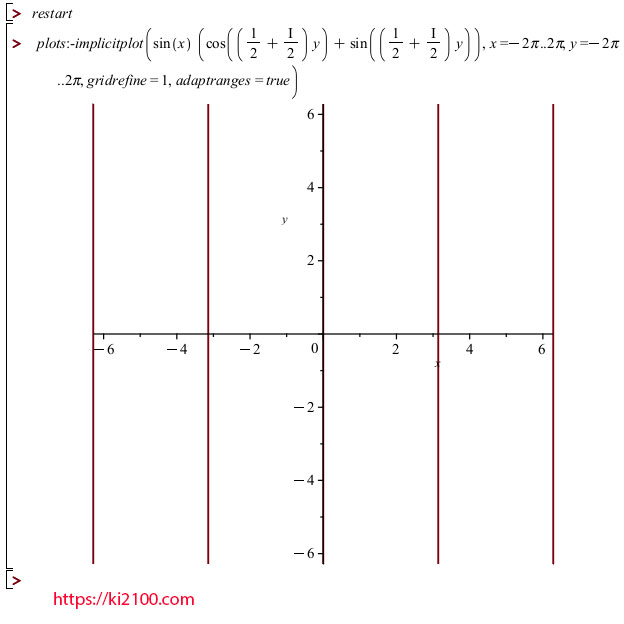
مختصات دوبعدی دکارتی:
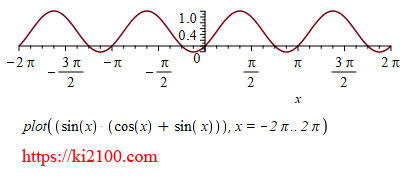
منطق
معادله میدان شرودینگر چیست؟
این تابع میدان، منطقی هامیلتونی یا لاگرانژی دارد. خوب
هامیلتونی یا ... چیست؟
در
مکانیک کلاسیک یا مکانیک منظومهای، سیارهای که بهدور خورشید در حال
چرخش است دو نوع نیرو دارد. نیروی جانب مرکز (گریزازمرکز) و نیروی
جاذبه مابین خودش و ستاره همچنین دو نوع انرژی دارد. انرژی پتانسیل
گرانشی که تابعی از جرم و فاصله است و انرژی جنبشی که تابعی از سرعت و
جرم است.
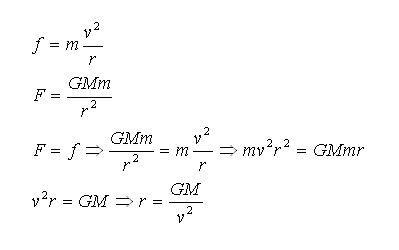

در
روش اول با برابرسازی نیروی جاذبه و گریزازمرکز، شعاع مدار و سرعت
سیاره محاسبه میشود؛ اما در روش هامیلتونی
یا لاگرانژی از تجمیع یا تفریق انرژی جنبشی و انرژی پتانسیل
گرانشی. در روش اول با نیرو سروکار داریم؛ ولی در روش های دوم با
انرژی. منطق هامیلتونی این است که تجمیع این دو انرژی در یک سامانه
منظومهای همواره مقدار ثابتی است.

خیلی ساده گفته باشیم در یک سیستم منظومهای انرژی جنبشی سیارات و
اقمار نصف انرژی پتانسیل گرانشی آنهاست. انیشتین مدعی بود که چیزی به نام
نیرو یا جاذبه چه گرانشی و چه الکتریکی و... وجود ندارد؛ بلکه واقعیت
انحنای فضا - زمان است. ازاینرو شاگرد ارشد او دیراک سعی کرد که دنیای
خرد و کوانتومی را بهوسیله معادله معروف خودش توجیه کند که آن هم منطق
هامیلتونی دارد. یعنی کل کیهان نسبیتی است:
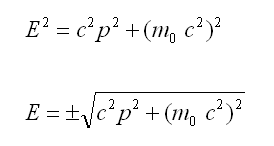
ازاینرو انیشتین سعی کرد که با واردکردن مفهوم انرژی - تکانه
یا انرژی - ضربه به معادلات تانسوری میدان خود، این انحنای فضا - زمان
را نشان دهد که یک دور باطل عقلانی بود؛ چون انرژی و ضربه خودشان
برگرفته از مفهوم اولیه و پایهای نیرو هستند که بعداً در مورد این
تدلیس انیشتین توضیحاتی ارائه خواهد شد. ولی شرودینگر میدانست که نه
انیشتین و نه دیراک هیچکدامشان موفق به توجیه و توضیح دنیای خرد یا
کوانتوم نمیشوند.

یعنی فرض شرودینگر این بود که ذرات باردار نیز همانند سیارات منظومهای
هستند با این تفاوت که دو انرژی دارند. انرژی اول جنبشی و ناشی از جرم
آنهاست و انرژی دوم الکتریکی و ناشی از بار الکتریکی یا پتانسیل میدان
الکتریکی است. این پتانسیل الکتریکی میتواند برای یک الکترون و درون
یک سیستم کوانتومی مثلاً اتم فرض شود و یا درون یک میدان الکتریکی فرضی
یا همان جعبه، چاه یا صد پتانسیل و... با استفاده از تجمیع یا تفریق
این دو سطح انرژی، میتوان معادله موج یا تابع موج را استخراج کرد.
معادلات یا توابع میدان شرودینگر حالت کلی داشته و هر فیزیکدانی
میتواند تحلیلها و مدلهای خاص خودش را داشته باشد. مهم این است که
کدام مدل در عمل و آزمونهای فیزیکی جواب دهد. به طور مثال:
محمدرضا طباطبایی
۱۳/۲/۱۴۰۱
https://www.ki2100.com

