آنالیز تانسور انیشتین
حل معادلات میدان نسبیت عام انیشتین
برای اولین و یکبار و برای همیشه
تانسور اینشتین:
پس از آنکه اینشتین به فکر
ارائه نظریه نسبیت عام خود بر مبنای رفع محدودیت‌های نسبیت خاص
(مخصوصاً ارتباط هندسی فضا - زمان) افتاد، اولین چالش پیش رویش
مقوله گرانش نیوتنی بود که بیان می‌نمود جاذبه یک عاملی خارجی است
و صرفاً بر اجرام تأثیر خواهد کرد. حال‌آنکه مطابق با نظریه نسبیت
خصوصی، جرم و انرژی دو تعریف (ظاهر) متفاوت از یک کمیت واحد هستند،
لذا تمامی خصوصیات مربوط به جرم شامل انرژی نیز خواهد شد. پس گرانش
نیز اگر بر اجرام اثر کرده و مسیر حرکت آنها را منحرف می‌کند،
بایستی مسیر حرکت بسته‌های انرژی متحرکت (کوانتوم‌های نوری) را نیز
منحرف نماید. این عمل به‌راحتی از طریق مشاهدات آرتور استنلی
ادینگتون مشهود بود با این تفاوت که مقادیر نتایج این مشاهدات
تقریباً دوبرابر پیش‌بینی نسبیت خاص بود؛ لذا اینشتین متوجه
محدودیت نسبیت خاص در خصوص نادیده‌گرفتن تغییرات در بازه زمانی شد؛
چراکه با نسبیت خاص تنها انحنای فضایی مدنظر گرفته می‌شود. پس این
ایده که اجرام ثقیل علاوه بر مکان، بر زمان مجاورشان نیز تأثیر
می‌گذارند، اولین‌بار این‌چنین به ذهن اینشتین خطور کرد و برای
توضیح ریاضیاتی آن بایستی از محاسبات تانسوری بهره بگیریم. بدین
منظور چون تانسور ریچی
نماد انحنا در فضا - زمان و تانسور تکانه - انرژی
نماد ماده (انرژی) در محاسبات تانسوری است، بایستی رابطه خطی میان
این دو برقرار باشد، اما چون مشتق هموردا (کواریانت)
صفر است:
مشتق هموردای طرف دیگر تساوی نیز باید صفر باشد که برای
این‌چنین نیست؛ لذا اینشتین جهت برطرف نمودن این مشکل ترکیبی از
ریچی و اسکالر ریچی R را از طریق اتحاد بیانکی به دست آورد که مشتق
کواریانت آن صفر است و به
تانسور اینشتین
معتبر است:
اگر خیلی ساده گفته باشیم بسیاری از تانسورها اولاً به‌صورت یک
عملگر ریاضی رفتار می‌کنند و ثانیا خروجی آنها یک جدول از داده و
اطلاعات است. منتها خیلی از این تانسورها جدول استاندارد و خاصی
ندارند که به‌روشنی تعریفش کنند. خروجی داده یا
اطلاعات تانسور انیشتین حداکثر ۱۰ تا است و نه بیشتر. ۶ تای دیگر
تکراری یا قرینه می‌شوند.
تانسور انیشتین هم این‌چنین وضعیتی دارد؛ یعنی یک عملگر تانسوری
روی متریک است؛ ولی جدول استانداردی ندارد که به‌درستی مشخص کند که
حاوی چه نوع اطلاعتی در کدامین اندیس است. چون تانسور ریچی به
انحنا مربوط می‌شود، استنباط اولیه هم این است که تانسور انیشتین
برگرفته شده از آن، حاوی اطلاعاتی در مورد انحنا خواهد بود.
تمامی خروجی‌های تانسور انیشتین نیاز به تحلیل و تفسیر دارند.
اینک روش یا پروسه آنالیز ما چیست؟
۱- معادله یا تابع چندین منیفلد یا خمینه را در مختصات
کروی پارامتری می‌کنیم.
۲- متریک آنها را به
دست می‌آوریم.
۳- تانسور یا عملگر
تانسوری انیشتین را به آن متریک اعمال می‌کنیم.
۴- خروجی و داده‌های
این تانسور را برسی و تحلیل می‌کنیم. در اول از کره شروع می‌کنیم.
بعد
از ریستارت کتابخانه فیزیک را فراخوانی کردیم. بعد تعریف متریک سه
تانسور انیشتین، ریچی و ریمان را اعمال کردیم و نتیجه صفر و تهی است.
این چگونه ممکن است؟ برای اینکه ما متریک یک کره با شعاع صفر یا بدون
شعاع را تعریف کردیم و باید به خود مقدار شعاع، اندازه بدهیم.
متریک ما اینک شبیه متریک شوارتس‌شیلد می‌شود و اولین چیزی که به چشم
می‌آید و شناسایی می‌شود، همان انحنای گاوسی یک کره است.
اینک چنبره:
این
بار به شعاع مقدار نمی‌دهیم. چون دو شعاع r,R داریم.
خروجی تانسور انیشتین دوبرابر انحنای گاوسی چنبره است.
اگر
یک جمع‌بندی کلی داشته باشیم اینکه، هر ریاضی - فیزیک‌دانی برای انحنا
یک تعریف خاصی داشته است. به طور مثال انحنای یک منحنی یا خم برابر است
با:
انحنای گاوسی می‌شود مجذور آن یعنی:
انحنای ژئودزینک هم با تعریف خاص خودش می‌شود:
و البته انحنای ریمان و ریچی و...
اینک سؤال این است که انیشتین در تئوری نسبیت عام خود از تعاریف قبلی
انحنا استفاده کرده یا سعی کرده است که تعاریف جدیدی ارائه کند؟
قدرمسلم تانسور انیشتین، متریک خمینه کروی را شناسایی نکرد یا بعد از
شناسایی انحنای آن را صفر ارائه کرد. با دادن مقدار برای شعاع، انحنای
ارائه شده همان انحنای گاوسی بود. ولی متریک چنبره را شناسایی و مقدار
انحنای آن را دوبرابر انحنای گاوسی ارائه کرد. مشکل در کجاست؟ متریک ها
تعاریف و مدل خاص خودشان را باید داشته باشند؟ یعنی متریک ها طبق سلیقه
نسبیت عام طرح و ارائه شوند؟ تانسور انیشتین فقط برای خمینه کروی است
یا تمام خمینه‌ها را قبول می‌کند؟
تمامی مشکلات و مصائب از اینجا ناشی می‌شود که خود انیشتین در کنار
معادلات میدان خود، کتابچه، جزوه یا دفترچه راهنمای استاندارد واضح و
روشنی ارائه نکرده است.
و
این کارکردن با آنها را دشوار و در نهایت غیرممکن می‌کند. در نهایت
باید الگوریتم منطقی نوشت که تمامی حالات ممکنه را تحت عملگر تانسوری
انیشتین قرارداده تا در نهایت به این نتیجه رسید که واقعاً این معادلات
ارزش علمی دارند و به کاری می‌آیند و یا اینکه صرفاً مدل‌سازی و
ناکارآمد و به‌دردنخور هستند.
در
مورد خمینه چنبره ما شعاع متریک را مثبت تعیین علامت کردیم که اگر
به‌صورت استاندارد متریک علامت‌گذاری منفی کنیم، تانسور انیشتین هم صفر
می‌شود.
اینک
اگر به شعاع مقدار دهیم انحنای گاوسی چنبره تا حد نسبتاً رضایت‌بخشی
اصلاح می‌شود؛
ولی
ما در یک میدان گرانشی با چیزی به نام انقباض طول یا همان کوتاه‌شدن
شعاع مواجه هستیم که باید آن را نیز لحاظ کنیم.
برای
اینکه معادلات میدان نسبیت عام انیشتین برای اولین و یکبار و برای
همیشه حل شوند ما از انقباض طول استفاده کرده و آن را جایگزین شعاع در
متریک یک خمینه کروی در مختصات کروی کردیم. مقادیر را برای ستاره
خورشید لحاظ کرده و خروجی تانسور انیشتین با اندیس ۲،۲ را در ده برابر
سرعت نور به توان دو ضرب کردیم. یعنی به‌جای جرم از ۱۰ برابر هم ارز و
معادل انرژی‌اش استفاده کردیم که دیگر هیچ نیازی به تانسور انرژی -
مومنتوم هم نیست. انحنای نور در سطح خورشید ۱.۶۲ ثانیه قوسی به دست
می‌آید. انیشتین آسوده بخواب که ما بیداریم. تانسورت حل شد.
راه‌حل نهایی از قرار زیر است:
علت
بر اینکه در معادله میدان از تانسور انرژی - تکانه استفاده شده و ما از
جرم استفاده کرده و به‌جای عدد ۸ از ۱۰ استفاده کردیم.
مسلماً با دورشدن از سطح خورشید، انحنای پرتو نور هم منحنی‌وار کاهش
پیدا می‌کند.
بعدازاین ما برای تانسور انیشتین یک جدول استاندارد واضح و روشنی
داریم. اندیس‌های ۱،۱ و ۴،۴ اشاره به انقباض طول و اتساع زمان دارند.
یعنی متر ما چقدر کوتاه و زمان ما چه‌قدر کند می‌شود.
اگر
تتا را پی دوم فرض کنیم اندیس ۳،۳ هم مشابه اندیس ۲،۲ یعنی همان زاویه
انحراف نور بر حسب رادیان است. دیگر هیچ ابهامی در مورد عملگر تانسوری
انیشتین باقی نماند. هر چهار درایه تانسور معلوم و مشخص شدند.
اندکی پس از انتشار نظریه نسبیت خاص در سال ۱۹۰۵، اینشتین در این
اندیشه بود که چگونه می‌تواند گرانش را در چارچوب نسبیتی جدیدش جای
دهد. در سال ۱۹۰۷ با شروع از یک آزمایش فکری شامل یک مشاهده‌گر در سقوط
آزاد، جستجویی هشت‌ساله برای دستیابی به نظریه‌ای نسبیتی برای گرانش را
آغاز کرد. پس از اشتباهات و انحرافات متعدد
سرانجام کار او در قالب آنچه امروزه معادلات میدان اینشتین می‌خوانیم،
حاصل داد و در نوامبر ۱۹۱۵ به آکادمی علوم پروشن ارائه شد. این معادلات
بیان می‌کنند که چگونه هندسهٔ فضا و زمان از کل ماده و تابش موجود
تأثیر می‌پذیرد و هسته نسبیت عام اینشتین را تشکیل می‌دهند.
معادلات میدان اینشتین غیرخطی هستند و ازاین‌رو یافتن پاسخ برای آنها
بسیار دشوار است. در حل مسائل مربوط به اولین پیش‌بینی‌های
نظریه‌اش، اینشتین از روش‌های تقریبی
استفاده نمود. اما دیری نپایید که در سال ۱۹۱۶ اخترفیزیک‌دانی
به نام کارل شوارتزشید نخستین پاسخ
غیربدیهی برای معادلات اینشتین را پیدا کرد که با نام متریک شوارتزشید
شناخته می‌شود. این پاسخ امکان توصیف مراحل نهایی رمبش گرانشی و
تشکیل اجسامی که امروزه به نام سیاه‌چاله می‌شناسیم، را فراهم نمود. در
همان سال نخستین گام‌ها برای تعمیم پاسخ شوارتزشید به اجسام باردار
آغاز شد. نتیجه این تلاش‌ها متریک
رایسنر-نوردشتروم بود که امروزه با سیاه‌چاله‌های دارای بار
الکتریکی مرتبط است. در سال ۱۹۱۷ اینشتین نظریه‌اش را در مورد جهان
به‌عنوان یک کل به کار گرفت و شاخه کیهان‌شناسی نسبیتی را پایه‌گذاری
نمود. در آن زمان اینشتین در راستای اندیشهٔ غالب عصر خود جهان را
ایستا می‌پنداشت و به همین دلیل پارامتر
جدیدی - ثابت کیهانی - را به معادلات اولیهٔ خود افزود تا بتواند آن
مشاهده را در نظریه‌اش تکرار نماید. اما تا سال ۱۹۲۹ در نتیجهٔ
کار هابل و سایرین مشخص شده بود که جهان ما در حال انبساط است. انبساط
جهان به‌خوبی توسط بسط جواب‌های کیهانی که توسط الکساندر فریدمان در
سال ۱۹۲۲ ارائه شد و نیازی به ثابت کیهانی ندارند، قابل‌توضیح است. با
استفاده از این جواب‌ها لومتر اولین نسخه از نظریه مهبانگ را
فرمول‌بندی کرد که در آن جهان از یک حالت بی‌نهایت داغ و چگال اولیه به
وجود آمده است. بعدها اینشتین ثابت کیهانی
را بزرگ‌ترین اشتباه زندگی خود خواند.
در خلال آن دوران، نسبیت
عام کنجکاوی بسیاری از فیزیک‌دانان نظری را برانگیخته بود. این نظریه
به‌وضوح از گرانش نیوتن برتر بود؛ زیرا با نسبیت خاص سازگار بود و از
عهده توضیح بسیاری از پدیده‌هایی برمی‌آمد که نظریه نیوتنی از توضیح
آنها ناتوان بود. خود اینشتین در سال ۱۹۱۵ نشان داد که چگونه نظریه‌اش
حرکت تقدیمی غیرعادی حضیض خورشیدی سیاره تیر را بدون استفاده از
هیچ‌گونه پارامتر اختیاری توجیه می‌کند. به طور مشابهی در سال ۱۹۱۹، طی
اکتشافی که توسط ادینگتون صورت گرفت، پیش‌بینی نسبیت عام در مورد
انحراف نور ستاره‌ها در طی خورشیدگرفتگی ۲۹ مه ۱۹۱۹، تأیید گردید و
باعث شهرت فوری اینشتین شد. اما تنها با گسترش‌هایی که بین سال‌های
۱۹۶۰ تا ۱۹۷۵ صورت گرفت این نظریه وارد جریان اصلی فیزیک نظری و
اخترفیزیک شد و ازاین‌رو، این دوره را عصر طلایی نسبیت عام می‌خوانند.
به‌تدریج فیزیک‌دانان مفهوم سیاه‌چاله را درک نمودند و اختروش‌ها را
به‌عنوان نمونه‌ای از تجلی اخترفیزیکی این مفهوم شناسایی کردند.
آزمایش‌هایی دقیق‌تر از همیشه بر روی منظومه شمسی قدرت پیش‌بینی نظریه
را تأیید کردند و گرایش‌هایی برای استفاده از کیهان‌شناسی نسبیتی برای
هدایت آزمایش‌های مشاهده‌ای به وجود آمد.
تحلیل ما این‌گونه است که انیشتین از راه آزمون و خطای فکری این
معادلات میدان خودش را ارائه نموده و هیچ راه و روش آزمایشگاهی برای آن
نداشته است. از همه مهم‌تر دست‌کاری تانسور ریچی و خود انیشتین نتوانست
هیچ جوابی برای معادلات خود ارائه کند. بزرگ‌ترین مشکل و چالش برای حل
این معادلات پیداکردن متریک مناسب برای اجرام سمای است. اولین پیشنهاد
توسط شوارتس‌شیلد بود؛ یعنی کنترل معادلات از دست خود انیشتین خارج و
به دست سایرین افتاده بود. خود انیشتین متوجه شده بود که این معادلات،
ابتدایی و دارای نواقصی هستند. پس به فکر واردکردن ثابتی به نام لامبدا
بود. ما بعد از تعریف و ارائه متریک جدیدی این ثابت لامبدا را ده برابر
سرعت نور به توان دو یعنی ده برابر هم ارز جرمی از نوع انرژی ضرب در
اندیس‌های ۲،۲ و ۳،۳ پیدا کردیم. یعنی انیشتین تا آخرین لحظات زندگی
خودش نسبت به این معادلات دو دل و مشکوک بوده است. بزرگ‌ترین تلاش
جهانی برای نجات معادلات میدان انیشتین همان تانسور انرژی - تکانه و
متریک تولمن است که با اعمال تانسور انیشتین، جواب‌ها تقریباً لاینحل
می‌شوند. یعنی گروهی از طرف‌داران انیشتین و نظریه نسبیت عام با سعی و
تلاش خود همت بر این گماشته بودند تا در مقابل منتقدین ایستادگی و
پایداری کنند و در عمل انیشتین معادلات میدان خود را به دیگران واگذار
کرده بود تا از آن دفاع کنند.
انیشتین به موسیقی و زدن ساز ویولن خیلی علاقه داشت. اگر او را
موسیقی‌دان فرض کنیم، او هرگز نت‌نویسی نکرده؛ بلکه یک ساز جدید طراحی
و معرفی کرده که هر کسی برای خودش نتی نوشته و سازی بزند و دیگران هم
برقصند. شما نت را در متریک می‌نگارید و تانسور انیشتین آن را
می‌نوازد.
اگر
فرض کنیم که ویولن تانسور ریچی است، تانسور انیشتین ویولن‌سل می‌شود.
چرا؟
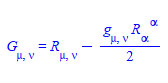
مشکل
دقیقاً اینجا بود که اولاً می‌بایست این ساز جدید را کوک کنند، یعنی
نیاز به ثابت یا بهتر است بگوییم ضریبی به نام لامبدا داشتند، ثانیاً
برای این ساز، نت‌نویسی می‌کردند؛ یعنی متریکی مناسب تعریف می‌کردند که
نه خود انیشتین و نه دوستانش و نه طرف‌داران نظریه نسبیت عام هرگز موفق
به انجام آن نیز نشدند و تمامی تلاش‌ها در نهایت بیهوده و در فرجام
شکست می‌خوردند. یعنی هیچ‌کس نتوانست که صدای دلنشینی از این ساز جدید
اختراع شده بیرون در آورد. تمامی بحث‌ها و مجادلات، بیهوده و بی‌فایده
و البته آزار دهند تمام می‌شدند.
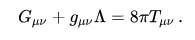
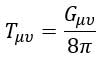
متریک شوارتس‌شیلد یا دوستی خاله‌خرسه. سکته مغزی دوم انیشتین و بحران
نسبیت عام.
ظاهراً شوارتس‌شیلد یکی از دوستان انیشتین و طرف‌داران نسبیت عام بود.
ازاین‌رو سعی کرد برای سیاه‌چاله‌ها متریکی وضع کند که توسط تانسور
انیشتین تحلیل شود.
این کار او خیلی شتاب‌زده بود؛ چون اولاً در مجامع علمی منتشر
شده بود و ثانیاً هیچ بخاری از تانسور انیشتین بلند نشد و همچنین
تانسور ریچی. ولی تانسور ریمان خروجی بسیار زیادی داشت و گردوخاک به پا
کرد و در مقابل تانسور انیشتین خودی نشان داد و عرض‌اندام کرد. در
نهایت گفتند که برای سیاه‌چاله‌های در شرف فروپاشی است که هیچ‌گونه
آثار گرانشی پیرامون خود ندارند که اگر داشتند، تانسور انیشتین حتماً
خروجی داشت. حالا بماند که این‌گونه سیاه‌چاله‌ها در کجای کیهان یافت
می‌شوند؟ یعنی کسی آدرس سراغ نداشت.
این
متریک انیشتین را کاملاً مأیوس و سرخورده کرد و بحرانی جدی در نظریه
نسبیت عام او به وجود آورد تا جای که خودش هم جرئت نکرد تا متریکی
تنظیم و معرفی کند چه برسد به اصلاح متریک شوارتس‌شیلد. سکوت برای او
بهترین دفاع بود.
بعد
از تشکیل جلسه اضطراری دوفوریتی چنین صورت‌جلسه کردند که انیشتین
طرف‌دار کیهان ایستا و پایدار و جاودانه است. او طرف‌دار فلسفه ازلی و
ابدی بودن کیهان است. ازاین‌رو خودش به شوارتس‌شیلد سفارش داده تا
متریکی وضع کند که معادله میدان او فلسفی شود. به نفع دنیای عالم و کل
بشیرت است که کیهان درجا بایستد و بزرگ هم نشود. اگر توسعه یابد
زمستان‌ها سردتر و سخت‌تر و اگر کوچک شود تابستان‌ها گرم‌تر است. همه
نیز از زحمات و الطاف او و شوارتس تشکر و قدردانی کردند. این دو
دانشمند منجی واقعی بوده و کیهان را از فروپاشی و بشر را از انقراض
نجات دادند.
اما در روزی ادوین هابل هم در محفل آنها حضور یافت و در جمع به
آن دو گفت که شما دو نفر چه غلطی کردید؟
آنها گفتند هیچ بلکه
تانسور انیشتین را پر از صفر کردیم که کیهان درجا بزند. ادوین گفت ای
احمق‌ها کیهان درجا نمی‌زند؛ بلکه با سرعتی نزدیک به‌سرعت نور در حال
انبساط و توسعه است. تا می‌توانید اعداد منفی وارد تانسور کنید. گویا
کیهان همچون فیل چرخیده و یک لیف شده است. کسی در جمع گفت تعداد صفرها
زیاد است یعنی ۱۶ تا. انیشتین گفت اشکالی ندارد یک عدد منفی را در کلش
ضرب می‌کنیم که قبل آن باید صفر را به یک تبدیل کنیم. تانسور خودمان
وارون تانسور ریچی است.
انیشتین بارها با خودش می‌گفت که دو بار جان سالم از سکته مغزی به در
بردم. جنگ جهانی، یهودی‌ستیزی و... به‌جای خود، چرا در دوران نقاهت دست
از سر من برنمی‌دارند. گویا این ساز ابداع کرده‌ام بلای جان خود من شده
و زمستان‌های سختی در پیش رو داریم و باید به فکر مکانی گرم‌ونرم و
بدون نیاز به هیزم و زغال‌سنگ بوده باشم؛ چون اگر هابل راست گفته باشد،
در گوشه ای از کیهان بسیار رقیق به سر خواهیم برد که هابل او را دلداری
داد که نترس، انبساط برون کهکشانی است و خود راه کهکشان به قول تو
ایستا است. بلد پروازی خودت را به داخل راه کهکشان محدود کن و فراتر از
آن نرو؛ چون سکته‌های بعدی در راه است و صدالبته زمستانی بسیار سرد و
سوزان برای نسبیت عام. راه شیری از ما محافظت می کند.
ولی آن کیست که از معادلات میدان تو حراست کند؛ چون بی‌دفاع
ماندند در مقابل ژرمن‌های یهودی‌ستیز. شرودینگر معادلات میدان خود را
شروع کرد و بعد از بسط و توسعه‌دادن حلشان کرد و جواب هم گرفت. تو راهی
را آغاز کردی نیمه‌کاره و از دیگران انتظار داری که حلش کنند و به
پایانش برسانند. قبول کن که اولاً اشتباه کردی ثانیاً شکست سختی خوردی.
چرا؟
شرودینگر در آزمایشگاهی حقیقی بود؛ ولی تو در آزمون‌های فکری غرق شدی
پس به فکر نجات‌غریق باش. خودکرده را تدبیر نیست.
واقعاً مشکل منطقی انیشتین در نسبیت عام چه بود. او ادعا می‌کرد شخصی
که در حال سقوط با شتاب g است، آثار گرانشی برای او صفر شده و از بین
هم می‌رود. ولی ما می‌دانیم که دو بردار شتاب g مثبت و منفی یکدیگر را
خنثی و صفر می‌کنند. یعنی شخصی که در ارتفاعی قرار دارد، تحت‌تأثیر
بردار شتاب گرانشی یا g منفی است. زمانی که سقوط می‌کند خودش شتاب g
مثبت اینرسی پیدا می‌کند و این دو بردار یکدیگر را خنثی می‌کنند. 0 = g
+ - g
ولی
او بعداً متوجه شد که با شتاب گرفتن، آثار گرانشی از بین نمی‌رود؛ چون
طول منقبض و زمان نیز کند می‌شود و عمده دلیل آن نه سرعت و شتاب، بلکه
خود میدان گرانش یا همان جی منفی است.
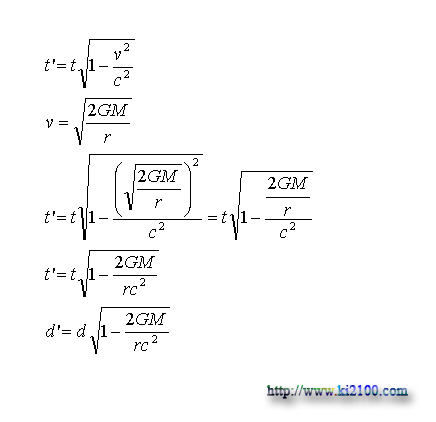
بحث
و محاسبات ما تا اینجا در یک محیط چهاربعدی ریمانی بود. اینک یک بعد
پایین‌تر آمده تا به محیط دوبعدی یک خمینه کروی نزدیک‌تر شویم. الان با
حذف زمان محیط ما سه‌بعدی ریمانی است.
متریک خمینه کروی در یک محیط سه‌بعدی ریمانی باز هم قابل‌شناسایی توسط
تانسور انیشتین نیست. اگر هم بوده باشد تمامی مقادیر صفر است. تصور
کنید که در یک مختصات سه‌بعدی دکارتی، فقط روی دو بعد یا محور دایره‌ای
رسم کردیم. اصولاً تمامی عملگرها روی این دایره اثر دارند. ولی در فضای
ریمانی این‌گونه نیست. فرض کنید که باید به دایره دوبعدی یک بعد دیگر
در امتداد محور سوم دهیم تا شبیه استوانه سه‌بعدی شود و سپس عملگرها
عمل کرده و خروجی دهند. اینک فرض کنید در محیط سه و چهاربعدی ریمانی ما
مجبور هستیم که یک کره دوبعدی را جابه‌جا کنیم تا شبیه یک کپسول شود.
در آن زمان تانسور انیشتین خروجی دارد. البته این کپسول ما خودش شبیه
یک کره است. دلیل اختلاف عددی 4.5 و 4.36 در این مسئله است. ولی چیز
زیاد مهمی نیست، چون اختلاف کم است و میتوان معدل گیری کرد.
آنالیز چیست؟
فرض کنید مهندس متالورژی آلیاژی تهیه و تولید کرده است. آزمایشگاه
آنالیز با منطق یا روش تولید متریال هیچ کاری ندارد و صرفاً ویژگی‌های
متالورژیکی قطعه را برسی می‌کند و اینکه به چه دردی می‌خورد و چه
کارایی دارد. آنالیز ریاضی هم این‌گونه است. ما فعلاً با منطق تانسور
انیشتین هیچ سروکاری نداریم و آن را یک محصول ریاضی فرض کرده و ورودی و
خروجی آن را برسی و تحلیل می‌کنیم و اینکه اصلاً چه کاربردی می‌تواند
داشته باشد. راهکار و ترفند ما تا اینجا این بود که اولاً یک خمینه
کروی دوبعدی را در بعد سوم r حرکت یا امتداد دهیم و ثانیاً انقباض طول
را به نسبت جرم و فاصله لحاظ کنیم.
حذف
تانسور انیشتین از قاموس فیزیک:
انحنای ریچی
در هندسه دیفرانسیل،
تنسور خمش ریچی،
انحنای ریچی
که برگرفته از نام گرگریو ریچی کورباسترو است، مقدار انحراف حجم یک گوی
ژئودزیک در یک خمینه ریمانی از حجم گوی استاندارد در فضای اقلیدسی را
نمایش می‌دهد. بدین ترتیب این تنسور راهی برای اندازه‌گیری میزان تفاوت
میان هندسه مشخص شده توسط متریک ریمانی با هندسه اقلیدسی معمولی
n-بعدی، فراهم می‌آورد. تنسور ریچی بر روی هر خمینه شبه ریمانی به‌صورت
اثری از تنسور خمش ریمان تعریف می‌شود. همانند خود متریک، تنسور ریچی
نیز یک‌شکل متقارن دوخطی در فضای مماس خمینه است (Besse 1987, p. 43).
در نظریه نسبیت، تنسور ریچی
بخشی از خمش فضا - زمان است که میزان تمایل ماده به واگرایی یا همگرایی
در زمان را مشخص می‌کند (از طریق معادله ریچادوری). این خمش توسط
معادلات میدان اینشتین به میزان کل ماده موجود در جهان مرتبط می‌گردد.
اگر تنسور ریچی در معادله خلأ اینشتین صدق کند، خمینه یک خمینه اینشتین
خواهد بود که بسیار موردمطالعه قرار گرفته است ((Besse 1987)). در این
اتصال، معادله شار ریچی بر تحوّل یک متریک به متریک اینشتین
حکم‌فرماست.
و
این سؤال مهم که چرا انیشتین از میان این همه تانسور تصمیم گرفت که
تانسور ریچی را انتخاب و آن را دست‌کاری و تغییر دهد.؟
اگر دقت کنید منیفلد
ما یک گوی یا کره استاندارد اقلیدسی با شعاع واحد یک است. پس انحنای
ریچی آن صفر می‌شود چون تمامی خمینه یا منیفلدهای دیگر به نسبت این یکه
سنجیده می‌شوند. یعنی انحنای آنها نسبت به انحنای این کره یکه. پس
منفیلد خودمان را باید به یک فضای سه‌بعدی بیضوی ریمانی منتقل کرده و
انقباض طول را تعریف کنیم.
هندسه ریمانی (به انگلیسی:
Riemannian Geometry)، شاخه‌ای از هندسه دیفرانسیل است، که به مطالعه
منیفلدهای ریمانی می‌پردازد، یعنی منیفلدهای هموار مجهز به متریک
ریمانی، این ساختار منیفلد را در هر نقطه مجهز به ضرب داخلی روی فضای
مماس می‌کند، به طوری که از نقطه‌ای به نقطه دیگر به طور هموار تغییر
می‌کند. همچنین این ساختار به طور خاص مفاهیم موضعی چون زاویه، طول خم،
مساحت رویه و حجم را به‌دست می‌دهد. از این‌ها، برخی از سایر کمیّت‌های
سرتاسری را میتوان به وسیله انتگرال‌گیری به‌دست آورد.
هندسه
ریمانی، از بینش برنهارت ریمان نشأت گرفت، که در نطق افتتاحیه خودش (با
عنوان «در مورد فرضیاتی که هندسه بر آن بنا نهاده شده») آن را بیان
داشت. این هندسه، تعمیم بسیار وسیع و مجردی از هندسه دیفرانسیل
رویه‌های درون R 3 رویه سه بعدی است. توسعه هندسه ریمانی منجر به ایجاد
نتایج متنوعی در ارتباط با هندسه رویه‌ها و رفتار ژئودزیک رویشان شد،
به همراه تکنیک‌هایی که میتوان از آنها در مطالعه منیفلدهای
دیفرانسیل‌پذیر ابعاد بالاتر استفاده کرد. این ساختار منجر به فرموله
کردن نسبیت عام انشتین شده و اثرات ژرفی را بر روی نظریه گروه‌ها،
نظریه نمایش، و آنالیز ایجاد کرده و موجب توسعه توپولوژی جبری و
توپولوژی دیفرانسیل گشته است.
فضای
خود را به یک سه‌بعدی ریمانی تغییر داده و متریک خود را تعریف می‌کنیم؛
ولی چون مقدار r اندازه ندارد، باز هم انحناها صفر است. پس مقدار r را
عامل انقباض طول در میدان گرانشی یعنی عددی مابین صفر و یک تعریف
می‌کنیم. اینک تانسورهای ریچی خروجی پیدا می‌کنند. یعنی منفیلد ما یک
بیضیگون مانندی شده است که با تغییر زاویه تتا، تغییر انحنا می‌دهد؛
ولی انحنای مدنظر ما در پی دوم است؛ یعنی جایی که سینوس تتا یک است.
اینک
جرم و شعاع و... خورشید را لحاظ می‌کنیم. انحنا بر حسب رادیان با ضریب
۸ به دست می‌آید یعنی ۱.۷۴ ثانیه قوسی. ولی یک مشکل داریم و آن اینکه
انحنا منفی است و برای مثبت کردن آن، از عامل اتساع زمان در میدان
گرانش استفاده می‌کنیم؛ یعنی عکس مقدار قبلی.
الان همه چیز تکمیله برای کنار گذاشتن دائمی و
ابدی تانسور انیشین و تانسور انرژی - مومنتوم و متریک تولمن و ....
تنها با دانستن جرم و فاصله از مرکز یک جرم سماوی کروی می‌توانیم زاویه
انحراف پرتور نور را با دقت بسیار بالایی پیدا کنیم. در نهایت برای
کالیبره کردن تابع، مقدار ضریب 8 را اندکی تغییر می‌دهیم تا برای تمامی
فواصل معتبر بوده باشند.
لازم به توضیح است که برای پیچیده نشدن مبحث فعلاً از عملیات انتگرال و
مشتق‌گیری از تانسورها خودداری کردیم.
کم‌کم داریم به پایان مبحث می‌رسیم و این سؤال مهم که چهاربعدی
شبه ریمانی انیشتین واقعاً چیست؟
طبق باور و تعاریف او ما در یک چهاربعدی فضا - زمان در مختصات کروی یک
بعد طولی، بعد تتا، بعد فی و بعد زمانی داریم. بعد فضایی یا طولی به
علت حضور جرم منقبض می‌شود و بعد زمانی اتساع می‌یابد. ازآنجایی‌که
انیشتین طرف‌دار دمکراسی و لیبرالیسم بود متریک معادله میدان خود را
آزاد و فری گذاشت تا هر انسان طبق سلیقه و خواست خودش یک متریک تعریف
کند و برای خودش یک کیهان سفارشی خلق کند. ولی به
لیبرالیسم هم احترام
گذاشت و گفت که باید مجلس عوام و اشراف انگلیس ساختمان خودشان را چند
روزی تخلیه و در اختیار گروهی از دانشمندان و ریاضی‌دانان معتبر
بگذارند و آنها رأی‌گیری کنند که کدام متریک معتبر است. آرای ۵۰ درصد
به‌اضافه یک باعث تصویب متریک جهانی می‌شود و امثال ادوین هابل هم
ممنوع‌الورود هستند. بعد تصویب متریک ملکه انگلیس زیر آن را مهر
پادشاهی زده و برای سازمان ملل نامتحد هم لازم‌الاجرا می‌شود و البته
که شورای امنیت هم حق وتوی آن را ندارد.
ولی
ما طبق منطق نسبیت عام جلو می‌رویم و متریک منطقی نسبیت عام را تعریف
می‌کنیم:
ابتدا نماد کریستوفل را به دست می‌آوریم. بعد آن تنسور انحنا و در
نهایت اسکار ریچی آن دو را به دست می‌آوریم که بیانگر انقباض کل معکوس
منیفلد ماست.
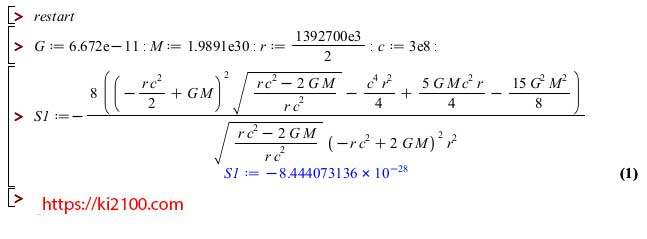
و این بزرگ‌ترین دست آورد بشریت در سایه نژاد اسرائیلی است که
در آلمان پرورش‌یافته که البته طبق قوانین لیبرالیسم نیاز به تأیید از
طرف گروهی کارشناس خبره دارد و این سؤال مهم که آیا این کارشناسان خبره
خودشان نمی‌توانند متریکی وضع و حل‌وفصل کرده و به جهانیان ارائه کنند.
خوب اگر می‌شد که خود انیشتین وضع و ارائه می‌کرد. قسمت جالب نسبیت عام
این است که حل نشود و هرگز به پایان نرسد؛ بلکه بهانه‌ای شود برای
جروبحث و مجادله و آموزش‌وپرورش، کلاس و درس‌ومشق و مکتب و... تخمه
شکستن، صرف تنقلات، تحقیق، پایان‌نامه، دکتری، فوق دکترا، کنفرانس،
بروبیا، گسترش صنایع توریسم و هتل‌داری و... چرا؟
چون ترکیب و تلفیقی از
فلسفه و فیزیک و ریاضیات است و به هیچ جایی هم نمی‌رسد. نتایج هر
آزمونی را میتوان با تفسیر فرمول‌بندی کرد. نتایج آزمون عوض شد،
تفسیرها نیز عوض می‌شوند. متریک و ثابت لامبدا همان مجسمه آزادی در
امریکا است.
درست
چیزی در مایه پیشگویی‌های نوستر آداموس است. هر اتفاقی که در دنیا روی
دهد با یک رباعی او همخوانی دارد. هر مشاهده‌ای در کیهان را میتوان با
نسبیت عام تفسیر کرد و ادعا کرد که نسبیت آن را از قبل پیشگوی کرده
است. اینک به نظر شما نوسترآداموس، انیشتین یا پیتر هیگز، کدام یک دست
بالای دست است.
پس نتیجه‌گیری نهایی ما اینکه در نسبیت عام دو اصل کلی داریم.
۱- آزادی یا دمکراسی در بیان، یعنی هر طور دلت خواست متریک و ثابت یا
ضریب لامبدا را تعریف کن.
۲- لیبرالیسم که برای جلوگیری از اغتشاش و آشوب است؛ یعنی بزرگان نسبیت
عام باید تشکیل جلسه داده و با کسب آرا ۵۰ درصد به‌اضافه یک به
اختلافات پایان دهند.
چرا این‌گونه شد؟ چون آلبرت یک یهودی زاده بود و مکتب یهودیت و
صهیونیست این‌گونه است. تمام یهودیان آزاد هستند که به‌وسیله عرفان
مرکاوا یا کابالا خدا، ملائکه، انبیا و... در کل شریعت را تعریف کنند.
در نهایت این بزرگان و خاخام‌های یهود هستند که با مراجعه به تورات
تحریف شده و جعلی حکم نهایی را صادر کنند و به اختلافات جامعه یهود
پایان دهند. یعنی نسبیت عام ادامه همام مکتب یهودیت و صهیونیست است که
در دو مجلس سنا و کنگره تعمیم‌یافته است.
اینک منتظر نظر پیشنهادی شما در
مورد متریک و ضریب لامبدا هستیم. خدا پدر نویسندگان میپل در کانادا را
بیامرزد؛ چون سه سوته هر تانسوری را که خواستید بر آن اعمال کرده و...
در نهایت می‌توانیم شاهد کیهان و... متصوره توسط شما بوده باشیم. زیاد
هم نظر خاخام‌های یهودی و بزرگان نسبیت عام و مجلس سنا و کنگره برای ما
مهم نیست مخصوصاً مجلس عوام و اشراف انگلیس حتی شورای امنیت سازمان ملل
نامتحد و هیئت‌های علمی و دانشگاهی یعنی اصلاً هیچ اهمیتی نیز ندارد؛
چون تا به امروز نتوانستند کاری از پیش ببرند. ما هم آزادی‌های مخصوص
به خود را داریم. به نظر شما کیهان کروی یا بیضوی است یا کپسولی یا
سوزنی یا شبیه زین اسب و... شاید هم تخم‌مرغی بوده باشد.
به یاد داشته باشید که قبل از مشاهدات عملی باید نبوغ خود را نشان دهید
که بعد از انجام مشاهدات، تفاسیر شما مورد قبول نیستند؛ چون ارزش
نخواهند داشت؛ چون چیزی در مایه سایر تفاسیر می‌شود و اصل سوم و نهایی
نسبیت عام پیشگویی است. یعنی باید پیشگویی خوبی داشته باشید و نه مفسر
عالی که تفسیر کار هر کسی است.
اگر
به ناسیونالیسم ایرانی یا پارسی علاقه دارید پیشنهاد ما متریک منشوری
است؛ یعنی ترکیب بیضوی و بیضیگون و استوانه.
حل
معادله میدان انیشتین در متریک تولمن.
روش
پیداکردن متریک شوارتس‌شیلد:
ریاضیات و هندسه
پیشرفته چیست؟
انسان برای حرکت از دو پا استفاده
کرده و بعداً از حیوانات چهاردست‌وپا. ولی بعداً چرخ را اختراع و گاری
و درشکه ساخته است. بعدها اسب و... حذف و دیگ بخار و موتور درون‌سوز
جای آن را گرفته است و هم اینک باطری و...
در ابتدا عملیات
دیفرانسیل روی چند متغیر خطی بوده است. بعدها روی توابع مثلثاتی و
زاویه. با پیشرفت بیشتر پارامترهای خطی حذف و عملیات دیفرانسیل روی یک
یا چند زاویه بر حسب رادیان صورت‌گرفته است. چرا؟
برای اینکه روی
منحنی‌ها، خم‌ها و خمینه‌ها یعنی اشکال و موجودات مدور کار می‌کردند.
چون دنیای پیرامونی ما و فیزیک این‌گونه است. نسبیت خاص روی گذر چیزی
به نام زمان متمرکز بوده است. یعنی زمان دامنه توابع محسوب می‌شده است.
این زمان خطی است یا چیزی شبیه زاویه؟
جواب هیچ‌کدام است؛ چون زمان
قابل مشاهد نیست؛ یعنی موجودی فیزیکی نیست. جریان وقتی عجیب شده که
نسبیت عام از هندسه دیفرانسیل استفاده کرده است و بجای دامنه اصلی
زاویه، از زمان استفاده کرده است. قبلاً ریمان متوجه شده بود که وقتی
ما معادله اشکال سه‌بعدی را پارامتری و تبدیل به متریک می‌کنیم یک بعد
کاهش داریم. معادله پارامتری شده کره سه‌جزئی است (سه‌بعدی دکارتی)؛
ولی متریک آن دوجزئی (دوبعدی تانسوری) می‌شود. ریمان ازاین‌رو جا برای
ابعاد بیشتر پیدا کرد و متریک های سه‌جزئی (سه اندیس) را ارائه نمود.
اما انیشتین واقعاً دست‌به‌کار عجیبی زده است؛ چون گذر زمان نه خطی و
نه دورانی یا چرخشی (زاویه‌ای) است و برای همگان سؤال این است که
خمینه‌های انیشتین چه شکلی هستند؟ آیا او دچار یک خطای اساسی و بنیادی
شده است؟
تانسورهای انیشتین چهار اندیس دارند و اگر به معادلات
دکارتی تبدیل شوند ۵ بعدی خواهند شد. یعنی یک افزایش در بعد. جریان
وقتی غامض می‌شود که زمان در یک اندیس بعد است؛ ولی در اندیس دیگر
دامنه تابع بعد دیگر تعریف شده است. درگیری چرخ و نعل اسب هم همیشه
مشهود است. یعنی عملیات دیفرانسیل هم بر روی زاویه است و هم بر روی
ابعاد. زمان گاهی دامنه است و گاهی برد.
کاربرد اول دیفرانسیل تحلیل داده و ارقام بود؛ اما بعداً در مورد تحلیل
اشیا و اجسام کاربرد پیدا کرد. آیا انیشتین سعی کرده داده و ارقام را
وارد اشیا و موجودات فیزیکی کند؟ آیا متوجه اصل قضیه دیفرانسیل و
کاربرد آن نبوده است؟ یعنی فرق موجود فیزیکال و آمار را نمی‌دانسته
است.
محمدرضا طباطبايي ۱۴۰۳/۰۴/۲۸
http://www.ki2100.com
